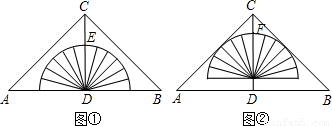
题目内容
 如图,半圆
如图,半圆 |
| AB |
 |
| AB |
 |
| AE |
 |
| BF |
 |
| EF |
分析:由弧AB为半圆,C为圆心,CD⊥AB,得到△ADB为等腰直角三角形,CA=CB=1,则AD=BD=
AB=
,∠EDF=90°,得到DE=DF=2-
,而S阴影部分AEFBDA的面积=S扇形DEF+S扇形BAE+S扇形ABF-S半圆AB-S△ADB,然后分别根据扇形和三角形的面积公式计算即可得到阴影部分AEFBDA的面积.
| ||
| 2 |
| 2 |
| 2 |
解答:解:∵弧AB为半圆,C为圆心,CD⊥AB,
∴△ADB为等腰直角三角形,CA=CB=1,
∴AD=BD=
AB=
,∠EDF=90°,
∴DE=DF=2-
,
∴S扇形DEF=
=
;
∴S阴影部分AEFBDA的面积=S扇形DEF+S扇形BAE+S扇形ABF-S半圆AB-S△ADB,
=
+2×
-
π×12-
×2×1,
=2π-
π-1.
∴△ADB为等腰直角三角形,CA=CB=1,
∴AD=BD=
| ||
| 2 |
| 2 |
∴DE=DF=2-
| 2 |
∴S扇形DEF=
90π×(2-
| ||
| 360 |
(3-2
| ||
| 2 |
∴S阴影部分AEFBDA的面积=S扇形DEF+S扇形BAE+S扇形ABF-S半圆AB-S△ADB,
=
(3-2
| ||
| 2 |
| 45π×22 |
| 360 |
| 1 |
| 2 |
| 1 |
| 2 |
=2π-
| 2 |
点评:本题考查了扇形的面积公式:S=
,其中n为扇形的圆心角的度数,R为圆的半径),或S=
lR,l为扇形的弧长,R为半径.也考查了圆周角定理及其推论.
| nπR2 |
| 360 |
| 1 |
| 2 |

练习册系列答案
相关题目
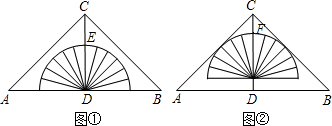 ②.则AB的边长为
②.则AB的边长为