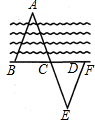题目内容
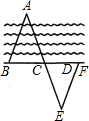
12、如图，A、B是位于河两岸的两个建筑物，要测量它们之间的距离，可以过点B画一条射线BF，在BF上取两点C、D，使CD=BC，再过点D作DE∥AB，使A、C、E在同一条直线上，根据△ABC≌△EDC知，测得DE的长就是A、B间的距离．这里说明△ABC≌△EDC的根据，除了ASA外，还可根据（ ）分析：根据DE∥AB，得出∠A=∠E，再由CD=BC，可证明△ABC≌△EDC，用全等三角形的推论AAS．
解答：解：∵DE∥AB，∴∠A=∠E，
∵CD=BC，∠ACB=∠ECD，
∴△ABC≌△EDC（AAS）．
故选A．
∵CD=BC，∠ACB=∠ECD，
∴△ABC≌△EDC（AAS）．
故选A．
点评：本题考查了全等三角形的判定和应用，是基础知识要熟练掌握．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
如图，A、B是位于河两岸的两个建筑物，要测量它们之间的距离，可以过点B画一条射线BF，在BF上取两点C、D，使CD=BC，再过点D作DE∥AB，使A、C、E在同一条直线上，根据△ABC≌△EDC知，测得DE的长就是A、B间的距离．这里说明△ABC≌△EDC的根据，除了ASA外，还可根据
