题目内容
【题目】（本题满分12分）已知：点E为AB边上的一个动点.
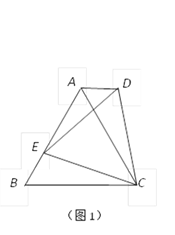
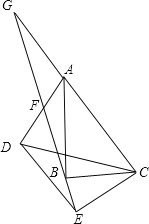
（1）如图1，若△ABC是等边三角形，以CE为边在BC的同侧作等边△DEC ，连结AD.试比较∠DAC与∠B的大小，并说明理由；
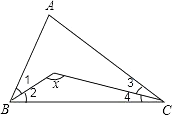
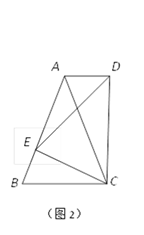
（2）如图2，若△ABC中，AB=AC，以CE为底边在BC的同侧作等腰△DEC ，且
△DEC∽△ABC，连结AD.试判断AD与BC的位置关系，并说明理由；
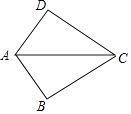
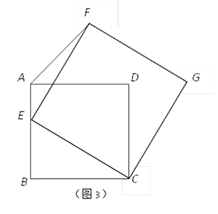
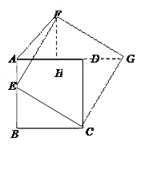
（3）如图3，若四边形ABCD是边长为2的正方形，以CE为边在BC的同侧作正方形ECGF.
①试说明点G一定在AD的延长线上；
②当点E在AB边上由点B运动至点A时，点F随之运动，求点F的运动路径长.
【答案】（1）∠DAC=∠B 理由见解析；（2）AD∥BC 理由见解析；（3）点F的运动路径长为
.
【解析】解：(1) ∠DAC=∠B 理由如下：
∵△ABC和△DEC都是等边三角形 ∴∠DCE=∠ACB=60° ∴∠BCE=∠ACD
∵BC=AC CE=CD ∴△BCE≌△ACD ∴∠B=∠DAC
（2）AD∥BC 理由如下：
∵△ABC和△DEC都是等腰三角形，且△DEC∽△ABC ∴
∵∠DCE=∠ACB ∴∠DCA=∠ECB ∴△DCA∽△ECB
∴∠DAC=∠EBC=∠ACB ∴AD∥BC
（3）①连结DG,∵四边形ABCD和FECG都是正方形
∴BC=CD CE=CG ∠BCD=∠ECG=90°
∴∠BCE=∠DCG∴△BCE≌△DCG …∴∠B=∠CDG=90°
∵∠ADC=90°∴∠ADC+∠CDG=180°
∴点G一定在AD的延长线上.
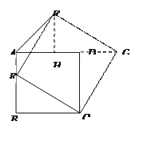
②作FH⊥AG于点H，易证：△FHG≌△GDC≌△EBC
∴FH=BE=DG HG=BC
∴AH=AG-GH=AD+DG-GH= BC+DG-BC=DG=FH
∴△AFH是等腰直角三角形
∴∠FAG=45°
∴点F的运动路径长=AC=
.
