Question

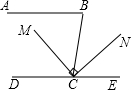如图，已知：AB∥DE，∠B=80°，CM平分∠BCD，CN⊥CM，则∠NCE的度数是________．

Answer 1

40°
分析：先根据AB∥DE，∠B=70°，CM平分∠DCB可求出∠BCM及∠BCE的度数，再根据CM⊥CN可求出∠BCN的度数，再由∠NCE=∠BCE-∠BCN即可解答．
解答：∵AB∥DE，∠B=80°，
∴∠DCB=180°-∠B=180°-80°=100°，∠BCE=∠B=80°，
∵CM平分∠DCB，
∴∠BCM=∠DCB=×100°=50°，
∵CM⊥CN，垂足为C，
∴∠BCN=90°-∠BCM=90°-50°=40°，
∴∠NCE=∠BCE-∠BCN=80°-40°=40°．
故答案为：40°．
点评：此题主要考查平行线的性质：两直线平行，内错角相等；两直线平行，同旁内角互补，属于基础题，注意细心掌握．