Question

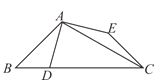
【题目】如图，△ABC中，∠ABC＝45°，∠BCA＝30°，点D在BC上，点E在△ABC外，且AD＝AE＝CE，AD⊥AE，则的值为____________．

Answer 1

【答案】

【解析】

过A点作BC的垂线，E点作AC的垂线，构造全等三角形，利用对应角相等计算得出∠DAM=15°，在AM上截取AG=DG，则∠DGM=30°，设DM=a,通过勾股定理可得到DG=AG=2a，GM=a,AM=BM=(，BD=(，AB=(,代入计算即可.

过A点作AM⊥BC于M点，过E点EN⊥AC于N点.

∵∠BCA＝30°，AE=EC

∴AM=AC，AN=AC

∴AM=AN

又∵AD=AE

∴RtADM RtAEN(HL)

∴∠DAM=∠EAN

又∵∠MAC=60°，AD⊥AE

∴∠DAM=∠EAN=15°

在AM上截取AG=DG，则∠DGM=30°

设DM=a,则 DG=AG=2a，

根据勾股定理得：GM=a,

∵∠ABC＝45°

∴AM=BM=(

∴BD=(，AB=(,

∴

故答案为：