题目内容
【题目】在Rt△ABC中，∠C=90°，AC=BC=1，将其放入平面直角坐标系，使A点与原点重合，AB在x轴上，△ABC沿x轴顺时针无滑动的滚动，点A再次落在x轴时停止滚动，则点A经过的路线与x轴围成图形的面积为 ．
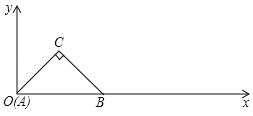
【答案】
【解析】
试题分析：
由勾股定理求出AB，由题意得出点A经过的路线与x轴围成的图形是一个圆心角为135°，半径为
的扇形，加上△ABC，再加上圆心角是90°，半径是1的扇形，由扇形的面积和三角形的面积公式即可得出结果.
试题解析：
解：∵∠C=90°，AC=BC=1，
∴AB=
；
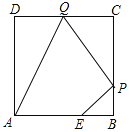
根据题意得：△ABC绕点B顺时针旋转135°，BC落在x轴上；△ABC再绕点C顺时针旋转90°，AC落在x轴上，停止滚动，
∴点A的运动轨迹是：先绕点B旋转135°，再绕点C旋转90°；如图所示：
∴点A经过的路线与x轴围成的图形是：一个圆心角为135°，半径为
的扇形，加上△ABC，再加上圆心角是90°，半径是1的扇形，
∴点A经过的路线与x轴围成图形的面积=
=；
故答案为：．
练习册系列答案
相关题目
【题目】宏远商贸公司有A、B两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：
体积（m3/件） | 质量（吨/件） | |
A型商品 | 0.8 | 0.5 |
B型商品 | 2 | 1 |
（1）已知一批商品有A、B两种型号，体积一共是20m3，质量一共是10.5吨，求A、B两种型号商品各有几件？
（2）物流公司现有可供使用的货车每辆额定载重3.5吨，容积为6m3，其收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；
②按吨收费：每吨货物运输到目的地收费200元．
要将（1）中的商品一次或分批运输到目的地，宏远商贸公司应如何选择运送、付费方式运费最少并求出该方式下的运费是多少元？
