题目内容
2、?ABCD的对角线AC，BD相交于点O，若△AOB的面积为6cm2，则?ABCD的面积为
24
cm2．分析：因为平行四边形的对角线互相平分，根据等底等高可知，△AOD、△COD、△BOC和△AOB的面积都相等，由此可以求出则?ABCD的面积．
解答：解：如图，∵?ABCD的对角线AC，BD相交于点O，
∴OA=OC，OB=OD，
∴S△AOD=S△COD=S△BOC=S△AOB，
而△AOB的面积为6cm2，
∴?ABCD的面积为4×6=24cm2．
故填空答案：24cm2．
∴OA=OC，OB=OD，
∴S△AOD=S△COD=S△BOC=S△AOB，
而△AOB的面积为6cm2，
∴?ABCD的面积为4×6=24cm2．
故填空答案：24cm2．
点评：此题主要考查了平行四边形的性质和等（同）底等高的三角形的面积相等．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
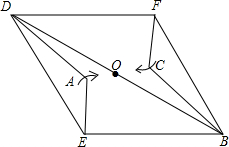DE、BF折叠四边形ABCD，A、C两点恰好都落在O点处，且四边形DEBF为菱形（如图）．
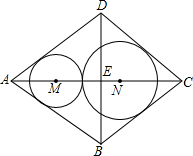形零件（菱形铁片上只能加工同一直径的零件，不计加工过程中的损耗），问加工哪种零件能最充分地利用这种铁片并说明理由．
如图，矩形ABCD的对角线AC，BD交于点O，∠AOD=120°，AC=12cm，则△ABO的面积是
23、菱形ABCD的对角线交于O点，DE∥AC，CE∥BD，求证：四边形OCED是矩形．
（2012•郴州）已知：点P是?ABCD的对角线AC的中点，经过点P的直线EF交AB于点E，交DC于点F．求证：AE=CF．