题目内容
等腰三角形的一个内角为38°，则它的一条腰上的高与底边的夹角为
19°或52°
19°或52°
．分析：当顶角为38°时和底角为38°两种情况进行求解．
解答：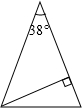
解：当顶角为38°时，底角为（180°-38°）÷2=71°．
此时它的一条腰上的高与底边的夹角为90°-71°=19°．
当底角为38°时，此时它的一条腰上的高与底边的夹角为90°-38°=52°．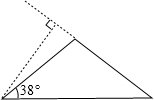
故答案为19°或52°．
解：当顶角为38°时，底角为（180°-38°）÷2=71°．此时它的一条腰上的高与底边的夹角为90°-71°=19°．
当底角为38°时，此时它的一条腰上的高与底边的夹角为90°-38°=52°．
故答案为19°或52°．
点评：本题考查等腰三角形的性质，等腰三角形中两个底角相等．同时考查了分类讨论的思想．
练习册系列答案
相关题目
已知等腰三角形的一个内角等于50°，则该三角形的一个底角的余角是（ ）
| A、25° | B、40°或30° | C、25°或40° | D、50° |