题目内容
如图l,在四边形A8CD中,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明).
(温馨提示:在图1中,连结BD,取BD的中点H,连结HE、HF,根据三角形中位线定理,可证得HE=HF,从而∠HFE=∠HEF,再利用平行线的性质,可证得∠BME=∠CNE.)
问题一:如图2,在四边形ADBC中,AB与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连结EF,分别交DC、AB于点M、N,判断△OMN的形状,请直接写出结论.
问题二:如图3,在△ABC中,AC>AB,D点在AC上,AB=CD,E、F分别是BC、AD的中点,连结EF并延长,与BA的延长线交于点G, 若∠EFC=600,连结GD,判断△AGD的形状并证明.

(1) 等腰三角形
(2) 直角三角线
证明:如图连接BD,取BD中点H,连接HF,HE


∴ △AGF是等边三角形.
∴ AF=FD.
∴ GF=FD.
∴ ∠FGI=∠FDG=300
∴ ∠AGD=900
即△AGD是直角三角形

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
 如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.
如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.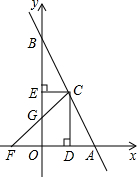 如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.
如图,已知直线AB经过点C(1,2),与x轴、y轴分别交于A点、B点,CD⊥x轴于D,CE⊥y轴于E,CF与x轴交于F.
