Question

如图，△ABC的面积为1，D、E为AC的三等分点，F、G为BC的三等分点．
求：（1）四边形PECF的面积；
（2）四边形PFGN的面积．

Answer 1

解：（1）△ABC的面积为1，D、E为AC的三等分点，F、G为BC的三等分点，
连接CP，设S_△PCF=x，S_△PCE=y．
则，
两式联立可得：x+y=，
即S_{四边形PECF}=；

（2）连NC，设S_△BGN=a，S_△CEN=b，
则S_△NCG=2a，S_△NEA=2b，
则，
解得a=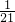，b=，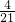
故S_{四边形PFGN}=S_△BEC-S_△BGN-S_{四边形PECF}=--=．
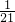分析：（1）连CP，设S_△PCF=x，S_△PCE=y，可建立关于x，y的方程组，解题的关键是把相关图形的面积用于x，y的代数式表示，并利用等分点导出隐含图形的面积；
（2）连NC，仿（1），先求出△BNC的面积，再得出△BNG面积，进而可求四边形PFGN的面积．
点评：本题考查三角形的面积结合二元一次方程组的应用，求一些关系复杂的图形面积，代数化是一个重要技巧，利用代数化，能清晰明朗地表示图形面积之间的关系，从而可以化解或降低问题的难度．