题目内容
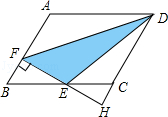
【题目】如图,在![]() 中,
中,![]() ,D是AB上的点,过点D作
,D是AB上的点,过点D作![]() 交BC于点F,交AC的延长线于点E,连接CD,
交BC于点F,交AC的延长线于点E,连接CD,![]() ,则下列结论正确的有______
,则下列结论正确的有______ ![]() 将所有正确答案的序号都填在横线上
将所有正确答案的序号都填在横线上![]()
![]() ;
;![]() ;
;![]() 是等边三角形;
是等边三角形;![]() 若
若![]() ,则
,则![]() .
.
【答案】![]()
【解析】
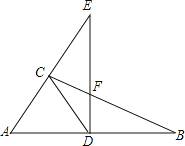
由在△ABC中,∠ACB=90°,DE⊥AB,易证得∠DCA=∠DAC,继而可得①∠DCB=∠B正确;
由①可证得AD=BD=CD,即可得②CD=![]() AB正确;
AB正确;
易得③△ADC是等腰三角形,但不能证得△ADC是等边三角形;
由若∠E=30°,易求得∠FDC=∠FCD=30°,则可证得DF=CF,继而证得DE=EF+CF.
∵在△ABC中,∠ACB=90°,DE⊥AB,
∴∠ADE=∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠DCB=90°,
∵∠DCA=∠DAC,
∴AD=CD,∠DCB=∠B;故①正确;
∴CD=BD,
∵AD=BD,
∴CD=![]() AB;故②正确;
AB;故②正确;
∠DCA=∠DAC,
∴AD=CD,
但不能判定△ADC是等边三角形;故③错误;
∵若∠E=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴∠ADC=30°,
∵∠ADE=∠ACB=90°,
∴∠EDC=∠BCD=∠B=30°,
∴CF=DF,
∴DE=EF+DF=EF+CF.故④正确.
故答案为:①②④.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目