题目内容
如图,直线l1:y=4x与直线 相交于点A,l2与x轴相交于点B,OC⊥l2,AD⊥y轴,垂足分别为C、D.动点P以每秒1个单位长度的速度从原点O出发沿线段OC向点C匀速运动,连接DP.设点P的运动时间为t(秒),DP2=S(单位长度2).
相交于点A,l2与x轴相交于点B,OC⊥l2,AD⊥y轴,垂足分别为C、D.动点P以每秒1个单位长度的速度从原点O出发沿线段OC向点C匀速运动,连接DP.设点P的运动时间为t(秒),DP2=S(单位长度2).(1)求点A的坐标;
(2)求S与t的函数关系式,并写出t的取值范围;
(3)在点P的运动过程中,DP能否为
 ?若能,求出此时的t值;若不能,说明理由.
?若能,求出此时的t值;若不能,说明理由.
【答案】分析:(1)由直线l1:y=4x与直线l2:y=- x+
x+ 相交于点A,联立可得方程组:
相交于点A,联立可得方程组: ,解此方程组即可求得点A的坐标;
,解此方程组即可求得点A的坐标;
(2)由OC⊥l2,即可求得直线OC的解析式,由OP=t,即可求得点P的坐标,由两点式,即可求得DP2的值,联立直线OC与直线l2:y=- x+
x+ ,即可求得点C的坐标,即可求得OC的长,即可得t的取值范围;
,即可求得点C的坐标,即可求得OC的长,即可得t的取值范围;
(3)由DP=4 与(2)中S与t的函数关系式,可得方程S=t2-6t+25=32,解此方程,又由0≤t≤4,即可判定点P的运动过程中DP不能为4
与(2)中S与t的函数关系式,可得方程S=t2-6t+25=32,解此方程,又由0≤t≤4,即可判定点P的运动过程中DP不能为4 .
.
解答:解:(1)∵直线l1:y=4x与直线l2:y=- x+
x+ 相交于点A,
相交于点A,
∴可得方程组: ,
,
解得: ,
,
∴点A的坐标为( ,5);
,5);
(2)∵点A的坐标为( ,5),
,5),
∴D(0,5),
∵OC⊥l2,直线l2的斜率为- ,
,
∴直线OC的斜率为 ,
,
∴直线OC的解析式为:y= x,
x,
联立直线OC与直线l2:y=- x+
x+ ,可得方程组:
,可得方程组: ,
,
解得: ,
,
∴点C的坐标为( ,
, ),
),
∴OC= =4,
=4,
∵OP=t(0≤OP≤OC),
过点P作PE⊥OB于E,
∵tan∠POE= ,
,
∴cos∠POE= ,sin∠POE=
,sin∠POE= ,
,
∴P点的坐标为( t,
t, t),
t),
∴DP2=( t-0)2+(
t-0)2+( t-5)2=t2-6t+25,
t-5)2=t2-6t+25,
∴S与t的函数关系为S=t2-6t+25(0≤t≤4);
(3)不能;
理由:若DP=4 ,
,
则S=DP2=(4 )2=32,
)2=32,
即S=t2-6t+25=32,
解得:t=7或t=-1(舍去),
∵0≤t≤4,
∴t=7不符合题意,
∴点P的运动过程中DP不能为4 .
.
点评:此题属于一次函数的综合题,考查了待定系数求一次函数解析式,两点式、函数交点问题以及方程组的解法.此题难度较大,注意掌握数形结合思想与方程思想的应用.
 x+
x+ 相交于点A,联立可得方程组:
相交于点A,联立可得方程组: ,解此方程组即可求得点A的坐标;
,解此方程组即可求得点A的坐标;(2)由OC⊥l2,即可求得直线OC的解析式,由OP=t,即可求得点P的坐标,由两点式,即可求得DP2的值,联立直线OC与直线l2:y=-
 x+
x+ ,即可求得点C的坐标,即可求得OC的长,即可得t的取值范围;
,即可求得点C的坐标,即可求得OC的长,即可得t的取值范围;(3)由DP=4
 与(2)中S与t的函数关系式,可得方程S=t2-6t+25=32,解此方程,又由0≤t≤4,即可判定点P的运动过程中DP不能为4
与(2)中S与t的函数关系式,可得方程S=t2-6t+25=32,解此方程,又由0≤t≤4,即可判定点P的运动过程中DP不能为4 .
.解答:解:(1)∵直线l1:y=4x与直线l2:y=-
 x+
x+ 相交于点A,
相交于点A,∴可得方程组:
 ,
,解得:
 ,
,∴点A的坐标为(
 ,5);
,5);(2)∵点A的坐标为(
 ,5),
,5),∴D(0,5),
∵OC⊥l2,直线l2的斜率为-
 ,
,∴直线OC的斜率为
 ,
,∴直线OC的解析式为:y=
 x,
x,联立直线OC与直线l2:y=-
 x+
x+ ,可得方程组:
,可得方程组: ,
,解得:
 ,
,∴点C的坐标为(
 ,
, ),
),
∴OC=
 =4,
=4,∵OP=t(0≤OP≤OC),
过点P作PE⊥OB于E,
∵tan∠POE=
 ,
,∴cos∠POE=
 ,sin∠POE=
,sin∠POE= ,
,∴P点的坐标为(
 t,
t, t),
t),∴DP2=(
 t-0)2+(
t-0)2+( t-5)2=t2-6t+25,
t-5)2=t2-6t+25,∴S与t的函数关系为S=t2-6t+25(0≤t≤4);
(3)不能;
理由:若DP=4
 ,
,则S=DP2=(4
 )2=32,
)2=32,即S=t2-6t+25=32,
解得:t=7或t=-1(舍去),
∵0≤t≤4,
∴t=7不符合题意,
∴点P的运动过程中DP不能为4
 .
.点评:此题属于一次函数的综合题,考查了待定系数求一次函数解析式,两点式、函数交点问题以及方程组的解法.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 20、如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,3),则关于x的不等式x+1≥mx+n的解集为
20、如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(a,3),则关于x的不等式x+1≥mx+n的解集为 如图,直线l1、l2交于点A,试求点A的坐标.
如图,直线l1、l2交于点A,试求点A的坐标. 如图,直线l1:y=2x+4与l2:y=-x-5在同一平面角坐标系中相交于点P,则点P的坐标是
如图,直线l1:y=2x+4与l2:y=-x-5在同一平面角坐标系中相交于点P,则点P的坐标是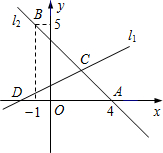 l2交于点C.
l2交于点C. 如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.
如图,直线l1,l2交于点A,直线l2与x轴交于点B,与y轴交于点D,直线l1所对应的函数关系式为y=-2x+2.