题目内容
如图，直线y=-| 4 | 3 |
（1）试说明△ABC是等腰三角形；
（2）动点M从A出发沿x轴向点B运动，同时动点N从点B出发沿线段BC向点C运动，运动的速度均为每秒1个单位长度．当其中一个动点到达终点时，他们都停止运动．设M运动t秒时，△MON的面积为S．
①求S与t的函数关系式；
②设点M在线段OB上运动时，是否存在S=4的情形？若存在，求出对应的t值；若不存在请说明理由；
③在运动过程中，当△MON为直角三角形时，求t的值．
分析：（1）求出x=0时y的值，求出y=0时x的值，求出B、C的坐标，根据勾股定理求出BC、AC，求出BA，即可得出答案；
（2）①过N作NH⊥x轴于H，推出当t=5秒时，同时到达终点，根据三角形的面积公式得出△MON的面积是S=
×OM×NH，代入求出即可；
②根据题意得出|t-2|×0.4t=4，根据t-2＞0，得出方程（t-2）×0.4t=4，求出方程的解即可；
③求出cos∠B=0.6，分为三种情况：I、当∠NOM=90°时，N在y轴上，求出t=5；II、当∠NMO=90°时，得出t-2=3-0.6t，求出t，III、∠MNO不可能是90°，即可得出答案．
（2）①过N作NH⊥x轴于H，推出当t=5秒时，同时到达终点，根据三角形的面积公式得出△MON的面积是S=
| 1 |
| 2 |
②根据题意得出|t-2|×0.4t=4，根据t-2＞0，得出方程（t-2）×0.4t=4，求出方程的解即可；
③求出cos∠B=0.6，分为三种情况：I、当∠NOM=90°时，N在y轴上，求出t=5；II、当∠NMO=90°时，得出t-2=3-0.6t，求出t，III、∠MNO不可能是90°，即可得出答案．
解答：（1）证明：y=-
x+4，
∵当x=0时，y=4；
当y=0时，x=3，
∴B（3，0），C（0，4），
∵A（-2，0），
由勾股定理得：BC=
=5，
∵AB=3-（-2）=5，
∴AB=BC=5，
∴△ABC是等腰三角形；
（2）解：①
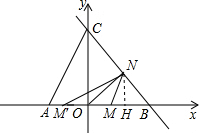∵C（0，4），B（3，0），BC=5，
∴sin∠B=
=
=0.8．
过N作NH⊥x轴于H．
∵点M从A出发沿x轴向点B运动，同时动点N从点B出发沿线段BC向点C运动，运动的速度均为每秒1个单位长度，
又∵AB=BC=5，
∴当t=5秒时，同时到达终点，
∴△MON的面积是S=
×OM×NH，
∴S=
|t-2|×0.8t，
∴S=|t-2|×0.4t；
②点M在线段OB上运动时，存在S=4的情形．理由如下：
∵C（0，4），B（3，0），BA=5，
∴sin∠B=
=
=0.8，
根据题意得：∵S=4，
∴|t-2|×0.4t=4，
∵点M在线段OB上运动，OA=2，
∴t-2＞0，
即（t-2）×0.4t=4，
即t2-2t-10=0，
解得：t=1+
，t=1-
（舍去），
∴点M在线段OB上运动时，存在S=4的情形，此时对应的t值是（1+
）秒．
③∵C（0，4）B（3，0）BC=5，
∴cos∠B=
=
=0.6．
分为三种情况：
I、当∠NOM=90°时，N在y轴上，即此时t=5；
II、当∠NMO=90°时，M、N的横坐标相等，即t-2=3-0.6t，解得：t=3.125，
III、∠MNO不可能是90°，
即在运动过程中，当△MON为直角三角形时，t的值是5秒或3.125秒．
| 4 |
| 3 |
∵当x=0时，y=4；
当y=0时，x=3，
∴B（3，0），C（0，4），
∵A（-2，0），
由勾股定理得：BC=
| 32+42 |
∵AB=3-（-2）=5，
∴AB=BC=5，
∴△ABC是等腰三角形；
（2）解：①
∵C（0，4），B（3，0），BC=5，∴sin∠B=
| OC |
| BC |
| 4 |
| 5 |
过N作NH⊥x轴于H．
∵点M从A出发沿x轴向点B运动，同时动点N从点B出发沿线段BC向点C运动，运动的速度均为每秒1个单位长度，
又∵AB=BC=5，
∴当t=5秒时，同时到达终点，
∴△MON的面积是S=
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
∴S=|t-2|×0.4t；
②点M在线段OB上运动时，存在S=4的情形．理由如下：
∵C（0，4），B（3，0），BA=5，
∴sin∠B=
| OC |
| BC |
| 4 |
| 5 |
根据题意得：∵S=4，
∴|t-2|×0.4t=4，
∵点M在线段OB上运动，OA=2，
∴t-2＞0，
即（t-2）×0.4t=4，
即t2-2t-10=0，
解得：t=1+
| 11 |
| 11 |
∴点M在线段OB上运动时，存在S=4的情形，此时对应的t值是（1+
| 11 |
③∵C（0，4）B（3，0）BC=5，
∴cos∠B=
| OB |
| BC |
| 3 |
| 5 |
分为三种情况：
I、当∠NOM=90°时，N在y轴上，即此时t=5；
II、当∠NMO=90°时，M、N的横坐标相等，即t-2=3-0.6t，解得：t=3.125，
III、∠MNO不可能是90°，
即在运动过程中，当△MON为直角三角形时，t的值是5秒或3.125秒．
点评：本题考查了一次函数图象上点的坐标特征，锐角三角函数的定义，等腰三角形的性质，直角三角形的性质，三角形的面积等知识点的应用，主要考查学生运用这些性质进行推理和计算的能力，用了方程思想，注意要进行分类讨论．
练习册系列答案
相关题目
12、如图，直线l1∥l2，AB⊥l1，垂足为O，BC与l2相交于点E，若∠1=43°，则∠2=
20、如图，直线AB∥CD，EF⊥AB，垂足为O，FG与CD相交于H，若∠1=43°，则∠2=
如图，直线AB与⊙O相切于点C，弦EF∥AB交OC于H，D是⊙O上一点，连接DE、DC、OF．
已知如图，直线y=-