题目内容
（2013•眉山）如图，△ABC中，E、F分别是AB、AC上的两点，且| AE |
| EB |
| AF |
| FC |
| 1 |
| 2 |
16
16
．分析：根据题意可判定△AEF∽△ABC，利用面积比等于相似比平方可得出△ABC的面积，继而根据S四边形EBCF=S△ABC-S△AEF，即可得出答案．
解答：解：∵
=
=
，
∴EF∥BC，
∴△AEF∽△ABC，
∴
=（
）2=（
）2=
，
∴S△ABC=18，
则S四边形EBCF=S△ABC-S△AEF=18-2=16．
故答案为：16．
| AE |
| EB |
| AF |
| FC |
| 1 |
| 2 |
∴EF∥BC，
∴△AEF∽△ABC，
∴
| S△AEF |
| S△ABC |
| AE |
| AB |
| 1 |
| 3 |
| 1 |
| 9 |
∴S△ABC=18，
则S四边形EBCF=S△ABC-S△AEF=18-2=16．
故答案为：16．
点评：本题考查了相似三角形的判定与性质，解答本题的关键是证明△AEF∽△ABC，要求同学们熟练掌握相似三角形的面积比等于相似比平方．
练习册系列答案
名题金卷系列答案
相关题目
（2013•眉山）如图是小强用八块相同的小正方体搭建的一个积木，它的左视图是（ ）
（2013•眉山）如图，∠BAC=∠DAF=90°，AB=AC，AD=AF，点D、E为BC边上的两点，且∠DAE=45°，连接EF、BF，则下列结论：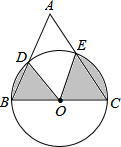
（2013•眉山）如图，以BC为直径的⊙O与△ABC的另两边分别相交于点D、E．若∠A=60°，BC=4，则图中阴影部分的面积为
（2013•眉山）如图，在函数y1=