题目内容
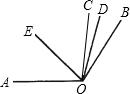 如图所示,已知∠AOB=120°,∠AOC是直角,OD平分∠BOC,OE平分∠AOC,求∠DOE的度数.
如图所示,已知∠AOB=120°,∠AOC是直角,OD平分∠BOC,OE平分∠AOC,求∠DOE的度数.
∠AOB=120°,∠AOC是直角,即∠AOC=90°,OE平分∠AOC,
则∠COE=45°,∠BOC=∠AOB-∠AOC=120°-90°=30°,
∵OD平分∠BOC,
∴∠COD=∠BOC÷2=30°÷2=15°,
∠DOE= ∠BOC+15°=60°.
∠BOC+15°=60°.
故答案为60°.
分析:利用角平分线的性质和图中角与角的关系计算.
点评:根据角平分线定义得出所求角与已知角的关系转化求解.
则∠COE=45°,∠BOC=∠AOB-∠AOC=120°-90°=30°,
∵OD平分∠BOC,
∴∠COD=∠BOC÷2=30°÷2=15°,
∠DOE=
 ∠BOC+15°=60°.
∠BOC+15°=60°.故答案为60°.
分析:利用角平分线的性质和图中角与角的关系计算.
点评:根据角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 25、如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
25、如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
 如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
如图所示,已知AO⊥BC于O,DO⊥OE,∠1=65°,求∠2的度数.
