题目内容
已知正方形ABCD中,点E在边DC上,DE=2,EC=1(如图所示),把线段AE绕点A旋转,使点E落在直线BC上的点F处,则F、C两点的距离为____________。
1或5
解析试题分析:如图,∵DE=2,EC=1,∴AB=BC=AD=DC=3,在Rt△ADE中,由勾股定理得AE= ,由旋转的性质可知,AF=AE=
,由旋转的性质可知,AF=AE= ,在Rt△ABF中,由勾股定理,得BF=
,在Rt△ABF中,由勾股定理,得BF= ,则FC=BC-BF=3-2=1;当F点在CB延长线上时,BF′=3+2=5.故答案为:1或5.
,则FC=BC-BF=3-2=1;当F点在CB延长线上时,BF′=3+2=5.故答案为:1或5.
考点:旋转的性质;勾股定理;正方形的性质.
点评:本题解题关键是利用勾股定理求线段长,利用旋转的性质得出AE=AF,本题注意F点在直线BC上的条件,分类讨论.

练习册系列答案
相关题目
 如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.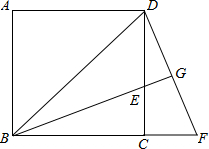 (2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G.
(2012•长沙)如图,已知正方形ABCD中,BE平分∠DBC且交CD边于点E,将△BCE绕点C顺时针旋转到△DCF的位置,并延长BE交DF于点G. 如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.
如图所示,已知正方形ABCD中的△DCF可以经过旋转得到△ECB.