题目内容
 用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是
用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠D′O′C′=∠DOC,需要证明△D′O′C′≌△DOC,则这两个三角形全等的依据是
- A.SAS
- B.SSS
- C.ASA
- D.AAS
B
分析:由作一个角等于已知角的方法得到O′D′=OD,O′C′=OC,C′D′=CD,利用SSS可得出△D′O′C′和△DOC全等,进而由全等三角形的对应角相等可得出∠D′O′C′=∠DOC,即可得到两三角形全等的依据为SSS.
解答:在△D′O′C′和△DOC中,
 ,
,
∴△D′O′C′≌△DOC(SSS),
∴∠D′O′C′=∠DOC.
则全等的依据为SSS.
故选B
点评:此题考查了全等三角形的判定与性质,以及作图-基本作图,全等三角形的判定方法有:ASA;SAS;SSS;AAS,以及HL(直角三角形判定全等的方法).
分析:由作一个角等于已知角的方法得到O′D′=OD,O′C′=OC,C′D′=CD,利用SSS可得出△D′O′C′和△DOC全等,进而由全等三角形的对应角相等可得出∠D′O′C′=∠DOC,即可得到两三角形全等的依据为SSS.
解答:在△D′O′C′和△DOC中,
 ,
,∴△D′O′C′≌△DOC(SSS),
∴∠D′O′C′=∠DOC.
则全等的依据为SSS.
故选B
点评:此题考查了全等三角形的判定与性质,以及作图-基本作图,全等三角形的判定方法有:ASA;SAS;SSS;AAS,以及HL(直角三角形判定全等的方法).

练习册系列答案
相关题目
 用直尺和圆规作一个角等于已知角,如图,能得出的依据是( )
用直尺和圆规作一个角等于已知角,如图,能得出的依据是( )| A、边边边 | B、边角边 | C、角边角 | D、角角边 |

 (2012•济宁)用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
(2012•济宁)用直尺和圆规作一个角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )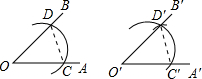 用直尺和圆规作一个角等于已知角的示意图如图所示,则说明△DOC≌△D'O'C'的依据是
用直尺和圆规作一个角等于已知角的示意图如图所示,则说明△DOC≌△D'O'C'的依据是