Question

【题目】在平面直角坐标系中，点.

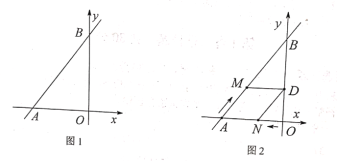
（1）直接写出直线的解析式；

（2）如图1，过点的直线交轴于点，若，求的值；

（3）如图2，点从出发以每秒1个单位的速度沿方向运动，同时点从出发以每秒0.6个单位的速度沿方向运动，运动时间为秒（），过点作交轴于点，连接，是否存在满足条件的，使四边形为菱形，判断并说明理由.

Answer 1

【答案】（1）；（2）或；（3）存在，

【解析】

（1）利用待定系数法可求直线AB解析式；

（2）分两种情况讨论，利用全等三角形的性质可求解；

（3）先求点D坐标，由勾股定理可得DN=AM=t，可证四边形AMDN是平行四边形，即当AM=AN时，四边形AMDN为菱形，列式可求t的值．

（1）设直线AB解析式为：y=mx+n，

根据题意可得：，

∴，

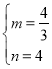∴直线AB解析式为；

（2）若点C在直线AB右侧，

如图1，过点A作AD⊥AB，交BC的延长线于点D，过点D作DE⊥AC于E，

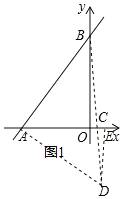
∵∠ABC=45°，AD⊥AB，

∴∠ADB=∠ABC=45°，

∴AD=AB，

∵∠BAO+∠DAC=90°，且∠BAO+∠ABO=90°，

∴∠ABO=∠DAC，AB=AD，∠AOB=∠AED=90，

∴△ABO≌△DAE（AAS），

∴AO=DE=3，BO=AE=4，

∴OE=1，

∴点D（1，-3），

∵直线y=kx+b过点D（1，-3），B（0，4）．

∴，

∴k=-7，

若点C在点A右侧时，如图2，

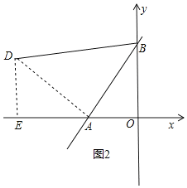
同理可得，

综上所述：k=-7或.

（3）设直线DN的解析式为：y=x+n，且过点N（-0.6t，0）,

∴0=-0.8t+n，

∴n=0.8t，

∴点D坐标（0，0.8t），且过点N（-0.6t，0），

∴OD=0.8t，ON=0.6t，

∴DN==1，

∴DN=AM=1，且DN∥AM，

∴四边形AMDN为平行四边形，

当AN=AM时，四边形AMDN为菱形，

∵AN=AM，

∴t=3-0.6t，

∴t=，

∴当t=时，四边形AMDN为菱形．