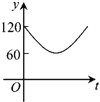
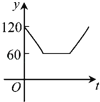
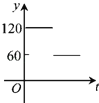
МвДҝДЪИЭ
ЎҫМвДҝЎҝ¶юҙОәҜКэ![]() Ј¬ЖдЦР
Ј¬ЖдЦР![]() Ј®
Ј®
ЈЁ1Ј©ЗуёГ¶юҙОәҜКэөД¶ФіЖЦб·ҪіМЈ»
ЈЁ2Ј©№э¶ҜөгC(0, ![]() )ЧчЦұПЯ
)ЧчЦұПЯ![]() ЎНyЦб.
ЎНyЦб.
ўЩ өұЦұПЯ![]() УлЕЧОпПЯЦ»УРТ»ёц№«№ІөгКұ, Зу
УлЕЧОпПЯЦ»УРТ»ёц№«№ІөгКұ, Зу![]() Ул
Ул![]() өДәҜКэ№ШПөЈ»
өДәҜКэ№ШПөЈ»
ўЪ ИфЕЧОпПЯУлxЦбУРБҪёцҪ»өгЈ¬Ҫ«ЕЧОпПЯФЪ![]() ЦбПВ·ҪөДІҝ·ЦСШ
ЦбПВ·ҪөДІҝ·ЦСШ![]() Цб·ӯХЫЈ¬НјПуөДЖдУаІҝ·ЦұЈіЦІ»ұдЈ¬өГөҪТ»ёцРВөДНјПу. өұ
Цб·ӯХЫЈ¬НјПуөДЖдУаІҝ·ЦұЈіЦІ»ұдЈ¬өГөҪТ»ёцРВөДНјПу. өұ![]() =7КұЈ¬ЦұПЯ
=7КұЈ¬ЦұПЯ![]() УлРВөДНјПуЗЎәГУРИэёц№«№ІөгЈ¬ЗуҙЛКұ
УлРВөДНјПуЗЎәГУРИэёц№«№ІөгЈ¬ЗуҙЛКұ![]() өДЦөЈ»
өДЦөЈ»
ЈЁ3Ј©Иф¶ФУЪГҝТ»ёцёш¶ЁөДxөДЦөЈ¬ЛьЛщ¶ФУҰөДәҜКэЦө¶јІ»РЎУЪ1Ј¬Зу![]() өДИЎЦө·¶О§Ј®
өДИЎЦө·¶О§Ј®
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј»ЈЁ2Ј©ўЩ
Ј»ЈЁ2Ј©ўЩ![]() Ј¬ўЪ
Ј¬ўЪ![]() Ј»ЈЁ3Ј©
Ј»ЈЁ3Ј©![]()
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©ҙъИл¶ФіЖЦб·ҪіМјҙҝЙЗуҪвЈ»
ЈЁ2Ј©ўЩЦұПЯlУлЕЧОпПЯЦ»УРТ»ёц№«№ІөгЈ¬Фт¶ҘөгөДЧЭЧшұкКЗnЈ¬јҙҝЙөГөҪmЎўnөД№ШПөЈ»
ўЪ ТАМвҝЙЦӘЈәөұ![]() КұЈ¬ЦұПЯ
КұЈ¬ЦұПЯ![]() УлРВөДНјПуЗЎәГУРИэёц№«№ІөгЈ¬ҙУ¶шҝЙЗуіцmөДЦөЈ»
УлРВөДНјПуЗЎәГУРИэёц№«№ІөгЈ¬ҙУ¶шҝЙЗуіцmөДЦөЈ»
ЈЁ3Ј©ПИЗуіцЕЧОпПЯөД¶ҘөгЧшұкЈ¬ёщҫЭМвТвөГіцІ»өИКҪЧйЈ¬ЗуҪвјҙҝЙ.
КФМвҪвОцЈәЈЁ1Ј©¶ФіЖЦб·ҪіМЈә ![]() .
.
ЈЁ2Ј©ўЩЎЯЦұПЯ![]() УлЕЧОпПЯЦ»УРТ»ёц№«№Іөг,
УлЕЧОпПЯЦ»УРТ»ёц№«№Іөг,
Ўа![]() .
.
ўЪ ТАМвҝЙЦӘЈәөұ![]() КұЈ¬ЦұПЯ
КұЈ¬ЦұПЯ![]() УлРВөДНјПуЗЎәГУРИэёц№«№Іөг.
УлРВөДНјПуЗЎәГУРИэёц№«№Іөг.
Ўа![]() .
.
ЈЁ3Ј©ЕЧОпПЯ![]() өД¶ҘөгЧшұкКЗ
өД¶ҘөгЧшұкКЗ![]() .
.
ТАМвҝЙөГ ![]()
ҪвөГ![]()
Ўа mөДИЎЦө·¶О§КЗ![]() .
.

 ФД¶БҝміөПөБРҙр°ё
ФД¶БҝміөПөБРҙр°ё