题目内容
【题目】如图,AB是⊙O的直径,BD,CD分别是过⊙O上点B,C的切线,且∠BDC=120°,连接AC. 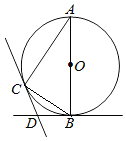
(1)求∠A的度数;
(2)若点D到BC的距离为2,那么⊙O的半径是多少?
【答案】
(1)解:连接OC,
∵BD,CD分别是过⊙O上点B,C的切线,
∴OC⊥CD,OB⊥BD,
∴∠OCD=∠OBD=90°,
∵∠BDC=120°,
∴∠BOC=360°﹣∠OCD﹣∠BDC﹣∠OBD=60°,
∴∠A= ![]() ∠BOC=30°
∠BOC=30°
(2)解:∵BD,CD分别是过⊙O上点B,C的切线,
∴DC=DB,
∴∠DCB=∠DBC= ![]() (180°﹣120°)=30°,
(180°﹣120°)=30°,
过点D作DE⊥BC,垂足为E,则DE=2,
∵∠DBC=30°,
∴BD=2DE=4,
在直角△DEB中, ![]() ,
,
∴BC=2BE= ![]() ,
,
由(1)可知△OBC为等边三角形,
∴OB=BC= ![]() ,
,
∴⊙O的半径是 ![]() .
.

【解析】(1)首先连接OC,由BD,CD分别是过⊙O上点B,C的切线,可求得∠BOC的度数,然后由圆周角定理,求得答案;(2)首先求得∠DCB与∠DBC的度数,然后过点D作DE⊥BC,垂足为E,则DE=2,即可求得BE的长,继而求得BC的长,然后由(1)可知△OBC为等边三角形,即可求得答案.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

练习册系列答案
相关题目





