题目内容
直角梯形的一条对角线把梯形分成两个三角形,若其中一个三角形是边长8cm的等边三角形,则这个梯形的面积是______.
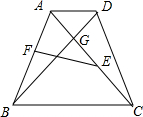
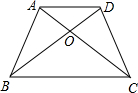
由题意可得如图:直角梯形ABCD,AC⊥CD,△BCD为等边三角形,边长为8cm,BE⊥CD为△BCD底边上的高.
∵直角梯形ABCD,AC⊥CD,BE⊥CD,
∴AB=CE,AC=BE;
在等边三角形BCD中,CE=ED=4cm(等边三角形边上的三线重合),
在Rt△BCE中,BE=
=
=4
;
∴梯形的面积=
(AB+CD)×BE=
(4+8)×4
=24
(cm2).
故答案为:24
cm2

∵直角梯形ABCD,AC⊥CD,BE⊥CD,
∴AB=CE,AC=BE;
在等边三角形BCD中,CE=ED=4cm(等边三角形边上的三线重合),
在Rt△BCE中,BE=
| BC2-CE2 |
| 82-42 |
| 3 |
∴梯形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:24
| 3 |


练习册系列答案
相关题目

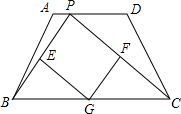
 于AB,AC于点E,点F,下列结论正确的是( )
于AB,AC于点E,点F,下列结论正确的是( )