题目内容
已知挂钟圆面上,分针长11cm(从圆心算起),那么从12点起到时针和分针第一次重合,分针末端走过的距离是cm.(圆周率π按3.14算)
- A.69.08
- B.74.84
- C.75.36
- D.76
C
分析:首先我们可以算出分针和时针下次相遇的时间为1点钟以后的时间.因此分针先走一圈,为2×11π=22π;然后从1点钟开始,设相遇时,分针走过的分钟数为a分钟,时针走过的分钟数为b分钟.因为分针走60分钟的距离时,时针走5分钟.所以速度比为60:5,即a:b=60:5,又因为分针比时针晚走5分钟,所以a-5=b.就算出a=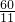 .也就是走了时钟一圈的
.也就是走了时钟一圈的 ,周长为2×11π×
,周长为2×11π× =2π.相加即可求解.
=2π.相加即可求解.
解答:从1点钟开始,设相遇时,分针走过的分钟数为a分钟,时针走过的分钟数为b分钟,则
 ,
,
解得a=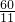 .
.
那么分针末端走过的距离为2×11π+2×11π× =22π+2π=24π=75.36.
=22π+2π=24π=75.36.
故选C.
点评:考查了二元一次方程组的应用,得出从12点起到时针和分针第一次重合,分针所走的时间是解题的关键.
分析:首先我们可以算出分针和时针下次相遇的时间为1点钟以后的时间.因此分针先走一圈,为2×11π=22π;然后从1点钟开始,设相遇时,分针走过的分钟数为a分钟,时针走过的分钟数为b分钟.因为分针走60分钟的距离时,时针走5分钟.所以速度比为60:5,即a:b=60:5,又因为分针比时针晚走5分钟,所以a-5=b.就算出a=
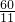 .也就是走了时钟一圈的
.也就是走了时钟一圈的 ,周长为2×11π×
,周长为2×11π× =2π.相加即可求解.
=2π.相加即可求解.解答:从1点钟开始,设相遇时,分针走过的分钟数为a分钟,时针走过的分钟数为b分钟,则
 ,
,解得a=
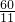 .
.那么分针末端走过的距离为2×11π+2×11π×
 =22π+2π=24π=75.36.
=22π+2π=24π=75.36.故选C.
点评:考查了二元一次方程组的应用,得出从12点起到时针和分针第一次重合,分针所走的时间是解题的关键.

练习册系列答案
相关题目
已知挂钟圆面上,分针长11cm(从圆心算起),那么从12点起到时针和分针第一次重合,分针末端走过的距离是( )cm.(圆周率π按3.14算)
| A、69.08 | B、74.84 | C、75.36 | D、76 |