题目内容
将二次函数y=x2﹣2x﹣3化成y=（x﹣h）2+k形式，则h+k结果为（ ）
| A．﹣5 | B．5 | C．3 | D．﹣3 |
D．
解析试题分析：y=x2-2x-3=（x2-2x+1）-1-3=（x-1） 2-4．
则h=1，k=-4，
∴h+k=-3．
故选D．
考点: 二次函数的三种形式．
练习册系列答案
名师点拨卷系列答案
相关题目
二次函数
的图象与
轴有两个交点，则
的取值范围是( )
A． | B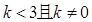． | C． | D． |
抛物线y=-(x-2)²+1经过平移后与抛物线y=-(x+1)²-2重合，那么平移的方向可以是（ ）
| A．向左平移3个单位后再向下平移3个单位； |
| B．向左平移3个单位后再向上平移3个单位； |
| C．向右平移3个单位后再向下平移3个单位； |
| D．向右平移3个单位后再向上平移3个单位。 |
二次函数y=ax2+bx+c的图象如图所示，则点
在（ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
二次函数y=2(x+1)2-3的图象的对称轴是（ ）
| A．直线x=-1 | B．直线x=1 | C．直线x=-3 | D．直线x=3 |
抛物线
的一部分如图所示，该抛物线在
轴右侧部分与
轴交点的坐标是（ ）．
| A．（0.5，0） | B．（1，0） | C．（2，0） | D．（3，0） |
与y=2(x-1)2+3形状相同的抛物线解析式为（ ）
A．y=1+ x2 | B．y=(2x+1)2 | C．y=(x-1)2 | D．y=2x2 |
，则这两个正方形的面积的和S关于
将抛物线y＝3x2向左平移2个单位，再向下平移1个单位，所得抛物线为（ ）
| A．y＝3（x＋2）2－1 | B．y＝3（x－2）2＋1 |
| C．y＝3（x－2）2－1 | D．y＝3（x＋2）2＋1 |