题目内容
【题目】如图,圆C过原点并与坐标轴分别交于A、D两点,已知点B为圆C圆周上一动点,且∠ABO=30°,点D的坐标为(0,2![]() ).
).
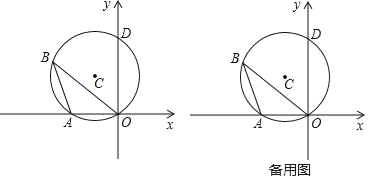
(1)直接写出圆心 C 的坐标;
(2)当△BOD为等边三角形时,求点B的坐标;
(3)若以点B为圆心、r为半径作圆B,当圆B与两个坐标轴同时相切时,求点B的坐标.
【答案】(1)(﹣1, ![]() );(2)B(﹣3,
);(2)B(﹣3, ![]() );(3)B(﹣
);(3)B(﹣![]() ﹣1,
﹣1, ![]() +1)或B(
+1)或B(![]() ﹣1,
﹣1, ![]() ﹣1).
﹣1).
【解析】试题分析:(1)连接OC并延长,交⊙C于点E,连接EA、ED,在直角三角形中,由30°角的性质和直角三角形的正切值可求出ED的长;再过点C作CF⊥OD,垂足为F,则CF是△DEO的中位线,根据三角形的中位线的性质可求C点的坐标;
(2)作BH⊥x轴交x轴于点H,根据勾股定理可求B点的坐标;
(3)分为B点在第一象限或第二象限,设出B的坐标,利用勾股定理可求解.
试题解析:(1)如图1,连接OC并延长,交⊙C于点E,连接EA、ED.
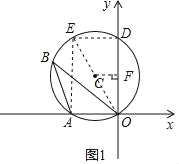
因为∠ABO=30°,
∴∠AEO=30°,又因为OE是直径,
∠AOE=60°,∠EOD=30°,∠EDO=90°
∵OD=2![]() ,
,
∴ED=DOtan30°=2.
过点C作CF⊥OD,垂足为F,则CF是△DEO的中位线,
所以OF=![]() ,CF=1.
,CF=1.
∴点C的坐标为(﹣1,![]() )
)
故圆心C的坐标为(﹣1,![]() );
);
(2)如图2,作BH⊥x轴交x轴于点H,
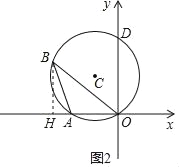
当△BOD是等边三角形,
则OB=OD=2![]() ,∠BOD=60°,
,∠BOD=60°,
故∠BOA=30°,
则BH=![]() OB=
OB=![]() ×2
×2![]() =
=![]() ,
,
OH=![]() =
=![]() =3,
=3,
∴B(﹣3,![]() );
);
(3
则BC=![]() ,
,
∴AD=![]() =
=![]() =4,
=4,
∴AC=2,
∵BC=AC,
∴![]() =2,
=2,
∴(﹣a+1)2+(a﹣![]() )2=4,
)2=4,
解得:a1=0(舍去),a2=1+![]() ,
,
故B(﹣![]() ﹣1,
﹣1,![]() +1),
+1),
若B在第一象限,设B(a,a),(a>0),
∴BC=![]() ,
,
同理:![]() =2,
=2,
解得:a3=0(舍去),a4=![]() ﹣1,
﹣1,
∴B(![]() ﹣1,
﹣1,![]() ﹣1),
﹣1),
综上所述:B(﹣![]() ﹣1,
﹣1,![]() +1)或B(
+1)或B(![]() ﹣1,
﹣1,![]() ﹣1).
﹣1).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了解某品牌轿车的熬油情况,将油箱加满后进行了耗油实验,得到如下数据:
轿车行驶的路程 |
|
|
|
|
| ··· |
油箱剩余油量 |
|
|
|
|
| ··· |
(1)该轿车油箱的容量为 ![]() ,行驶
,行驶![]() 时,油箱剩余油量为
时,油箱剩余油量为 ![]()
(2)根据上表的数据,写出油箱剩余油量![]() 与轿车行驶的路程
与轿车行驶的路程![]() 之间的表达式
之间的表达式![]() .
.
(3)某人将油箱加满后,驾驶该轿车从![]() 地前往
地前往![]() 地,到达
地,到达![]() 地时油箱剩余油量为
地时油箱剩余油量为![]() ,求
,求![]() 两地之间的距离?
两地之间的距离?