Question

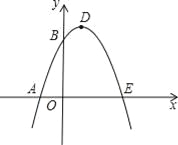
【题目】已知抛物线的解析式为，（与轴交于点（点在点左侧），与轴交于点，项点为．

（1）求点的坐标；

（2）若将抛物线沿着直线的方向平移得到抛物线；

①当抛物线与直线只有一个公共点时，求抛物线的解析式；

②点是①中抛物线上一点，若且为整数，求满足条件的点的个数．

Answer 1

【答案】（1）点，点，点，点；（2）①，②满足条件的点有个．

【解析】

（1）令y=0求出x，可得点A、B的坐标；令x=0求出y，可得点D的坐标；将二次函数的解析式化为顶点式即可得点P的坐标；

（2）①先求出直线PD的解析式，由抛物线的顶点在直线PD上移动可设出抛物线的顶点式，根据抛物线与直线只有一个公共点，利用可求得抛物线的顶点坐标，即可求得其解析式；

②先求出当、时的取值，根据二次函数的顶点式及其图象性质可分别求得当、时的取值范围，进而得出的整数值，即可求出满足条件的点的个数．

解：（1）取，即

解得：

则点，点

取，得

则点

又

则点

（2）①设直线的解析式为

点，点

解得

直线的解析式为，

抛物线沿着直线 的方向平移得到抛物线

平移后的顶点坐标为

设平移后解析式为

又抛物线与直线只有一个公共点

令

整理得：

则，即

解得

平移后所得抛物线的解析式为

即

②的顶点为

∵当时，时

∴当时，

则有个整数

当时，

则有个整数

抛物线是连续的，所以可以取到当时的函数值的所有整数，

故满足条件的点有个．