题目内容
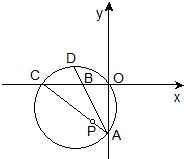23、如图，在直角坐标系中，点B、C在x轴的负半轴上，点A在y轴的负半轴上，以AC为直径的圆与AB的延长线交于点D，CD=AO，如果AO＞BO，且AO、BO是关于x的二次方程x2-14x+48=0的两个根．（1）求点D的坐标；
（2）定义：在直角坐标系中，有点M（m，n），对于直线y=kx+b，当x=m时，y=km+b＞n，则称点M在直线下方；当x=m时，y=km+b=n，则称点M在直线上；当x=m时，y=km+b＜n，则称点M在直线上方．
请你根据上述定义解决下列问题：
若点P在直径AC所在直线上，且AC=4AP，直线l经过点P和Q（6，-16），请你判断点D和直线l的位置关系．
分析：本题主要考查数形结合，有很强的逻辑能力．先根据AO＞BO，且AO、BO是关于x的二次方程x2-14x+48=0的两个根求出OA、OB的长，由三角形性质即可得D点坐标．第（2）问分两种情况进行分别讨论，从而判断出点D和直线l的位置关系．
解答：解：（1）∵AO＞BO，且AO、BO是关于x的二次方程x2-14x+48=0的两个根．
∴OA=8，OB=6
设D点坐标为（x，y）
求出OA=8，OB=6（1分）
求出点D的横坐标x=-9.6（1分）
纵坐标y=4.8（1分）
点D的坐标（-9.6，4.8）（1分）
（2）第一种情况：
当点P在线段AC上时，点P的坐标为（-4，-6）（1分）
得出直线l的解析式：y=-x-10（1分）
得出点D在直线l的上方．（1分）
第二种情况：
当点P在CA的延长线上时，点P的坐标为（4，-10）（1分）
得出直线l的解析式：y=-3x+2（1分）
得出点D在直线l的下方．（1分）
没有分类的情况下写出上方或下方不给分；有分类但没有说理过程，给答案（2分）．
∴OA=8，OB=6
设D点坐标为（x，y）
求出OA=8，OB=6（1分）
求出点D的横坐标x=-9.6（1分）
纵坐标y=4.8（1分）
点D的坐标（-9.6，4.8）（1分）
（2）第一种情况：
当点P在线段AC上时，点P的坐标为（-4，-6）（1分）
得出直线l的解析式：y=-x-10（1分）
得出点D在直线l的上方．（1分）
第二种情况：
当点P在CA的延长线上时，点P的坐标为（4，-10）（1分）
得出直线l的解析式：y=-3x+2（1分）
得出点D在直线l的下方．（1分）
没有分类的情况下写出上方或下方不给分；有分类但没有说理过程，给答案（2分）．
点评：本题主要考查数形结合，是函数和图形的有机结合，特别是第（2）问需要给出分类情况进行讨论．
练习册系列答案
相关题目
如图，在直角坐标系中，点P的坐标为（3，4），将OP绕原点O逆时针旋转90°得到线段OP′．
，2）．画出△ABC的两个位似图形△A1B1C1，△A2B2C2，同时满足下列两个条件：