题目内容
若等腰梯形的上底、高、下底分别为2cm、2cm、6cm，则这个等腰梯形中的锐角等于________．
45°
分析：过点C作CE⊥AB，则可得出AE的长度，再由tan∠A的值，可得出∠A的度数．
解答：
解：由题意得，CD=2cm，CE=2cm，
∵四边形ABCD是等腰梯形，
∴AE=
（AB-CD）=2cm，
在RT△ACE中，tan∠A=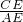
=1，
故可得∠A=45°．
故答案为：45°．
点评：此题考查了等腰梯形的性质，根据等腰梯形的性质得出AE的长度是解答本题的关键，难度一般．
分析：过点C作CE⊥AB，则可得出AE的长度，再由tan∠A的值，可得出∠A的度数．
解答：
解：由题意得，CD=2cm，CE=2cm，∵四边形ABCD是等腰梯形，
∴AE=
（AB-CD）=2cm，在RT△ACE中，tan∠A=
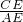=1，故可得∠A=45°．
故答案为：45°．
点评：此题考查了等腰梯形的性质，根据等腰梯形的性质得出AE的长度是解答本题的关键，难度一般．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目