题目内容
以两条边长为9和2及另一边组成边长都是整数的三角形一共有（ ）
| A、3个 | B、4个 |
| C、5个 | D、无数多个 |
考点：三角形三边关系,一元一次不等式组的整数解
专题：
分析：首先根据三角形的三边关系可得9-2＜第三边＜9+2，再解不等式，求出整数解即可．
解答：解：设第三边长为x，由题意得：
9-2＜x＜9+2，
解得：7＜x＜11，
∵x为整数，
∴x=8，9，10，
故选：A．
9-2＜x＜9+2，
解得：7＜x＜11，
∵x为整数，
∴x=8，9，10，
故选：A．
点评：此题主要考查了三角形的三边关系，关键是掌握第三边的范围是：大于已知的两边的差，而小于两边的和．
练习册系列答案
相关题目
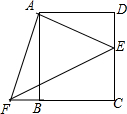如图，在正方形ABCD中，E、F分别是CD和CB的延长线上的点，且DE=BF，连结AE、AF．
在平面直角坐标系中，△ABC的位置如图所示，将△ABC先向左平移3个单位，再作出其关于x轴的对称图形，则A点的对应点的坐标为（ ）| A、（-3，-2） |
| B、（-1，-2） |
| C、（-2，-2） |
| D、（-2，-3） |
观察下列标志，不是中心对称图形的是（ ）
A、 |
B、 |
C、 |
D、 |