题目内容
21、如图所示，在△MNP中，H是高MQ与NE的交点，且QN=QM，猜想PM与HN有什么关系？试说明理由．
分析：首先根据等角的余角相等，得出∠EMH=∠QNH，再利用ASA定理证明△MPQ≌△NHQ，从而得出MP=NH．
解答：证明：PM=HN．∵∠MEH=∠NQH=90°（垂直的定义），
∠MHE=∠NHQ（对顶角相等），
∴∠EMH=∠QNH（等角的余角相等）
MQ=NQ（已知）
∠MQP=∠NQH=90°（已知）
∴△MPQ≌△NHQ，∴MP=NH．
∠MHE=∠NHQ（对顶角相等），
∴∠EMH=∠QNH（等角的余角相等）
MQ=NQ（已知）
∠MQP=∠NQH=90°（已知）
∴△MPQ≌△NHQ，∴MP=NH．
点评：解答本题的关键是根据ASA判定△MPQ≌△NHQ．
练习册系列答案
相关题目
在如图所示的网格中，△MNP绕某点旋转一定角度，得到△M1N1P1，其旋转中心可能是（ ）
如图所示，在△MNP中，H是高MQ与NE的交点，且QN=QM，猜想PM与HN有什么关系？试说明理由．
、
、
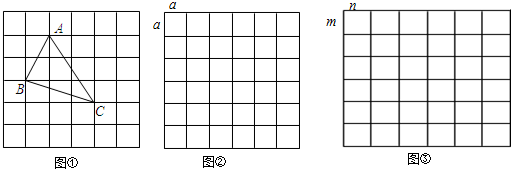
，求这个三角形的面积．”小明同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图①所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．我们把上述求△ABC面积的方法叫做构图法．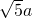
、
、
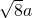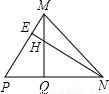
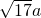（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△DEF，并直接写出它的面积．
、
、
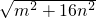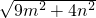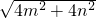（m＞0，n＞0，且m≠n），试运用构图法求出△MNP的面积．
