题目内容
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以每秒2cm的速度在线段AB上由A向B匀速运动,E点同时以每秒1cm的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t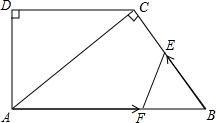 <5).
<5).
(1)求证:△ACD∽△BAC;
(2)求DC的长;
(3)设四边形AFEC的面积为y,用含t的代数式表示y,并探究何时四边形AFEC的面积最小.
解:(1)∵AB∥DC,
∴∠ACD=∠BAC.
∵AC⊥BC,
∴∠D=∠ACB=90°.
∴△ACD∽△BAC;
(2)在Rt△ABC中,AB=10,BC=6,
∴AC=8.
∵△ACD∽△BAC,
∴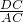 =
= .
.
∴DC=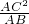 =
=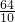 =
= (cm);
(cm);
(3)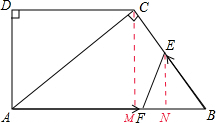
作CM⊥AB于点M,EN⊥AB于点N.
∵S△ABC= AC•BC=
AC•BC= AB•CM,
AB•CM,
∴CM= =
=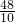 =
= .
.
∵CM∥EN,
∴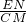 =
= ,
,
∴EN=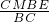 =
=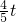 .
.
S四边形AFEC=S△ABC-S△BEF
= ×6×8-
×6×8- ×(10-2t)×
×(10-2t)× t
t
=24-4t+ t2,
t2,
即 y= t2-4t+24.(0<t<5)
t2-4t+24.(0<t<5)
∵ >0,∴y有最小值.
>0,∴y有最小值.
当t=- =2.5时,y值最小.
=2.5时,y值最小.
分析:(1)由∠D=∠ACB,∠ACD=∠BAC可得证;
(2)运用相似三角形性质计算;
(3)四边形AFEC的面积=△ABC的面积-△BEF的面积.
点评:此题考查动态问题中相似三角形的判定与性质和二次函数的综合应用,正确表示△BEF的面积是关键.难度中等.
∴∠ACD=∠BAC.
∵AC⊥BC,
∴∠D=∠ACB=90°.
∴△ACD∽△BAC;
(2)在Rt△ABC中,AB=10,BC=6,
∴AC=8.
∵△ACD∽△BAC,
∴
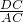 =
= .
.∴DC=
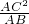 =
=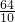 =
= (cm);
(cm);(3)

作CM⊥AB于点M,EN⊥AB于点N.
∵S△ABC=
 AC•BC=
AC•BC= AB•CM,
AB•CM,∴CM=
 =
=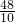 =
= .
.∵CM∥EN,
∴
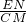 =
= ,
,∴EN=
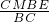 =
=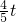 .
.S四边形AFEC=S△ABC-S△BEF
=
 ×6×8-
×6×8- ×(10-2t)×
×(10-2t)× t
t=24-4t+
 t2,
t2,即 y=
 t2-4t+24.(0<t<5)
t2-4t+24.(0<t<5)∵
 >0,∴y有最小值.
>0,∴y有最小值.当t=-
 =2.5时,y值最小.
=2.5时,y值最小.分析:(1)由∠D=∠ACB,∠ACD=∠BAC可得证;
(2)运用相似三角形性质计算;
(3)四边形AFEC的面积=△ABC的面积-△BEF的面积.
点评:此题考查动态问题中相似三角形的判定与性质和二次函数的综合应用,正确表示△BEF的面积是关键.难度中等.

练习册系列答案
相关题目
 20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈
20、如图,在直角梯形ABCD中,AD∥BC,CD⊥BC,E为BC边上的点.将直角梯形ABCD沿对角线BD折叠,使△ABD与△EBD重合(如图中阴影所示).若∠A=130°,AB=4cm,则梯形ABCD的高CD≈ 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5).
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,AC⊥BC,AB=10cm,BC=6cm,F点以2cm/秒的速度在线段AB上由A向B匀速运动,E点同时以1cm/秒的速度在线段BC上由B向C匀速运动,设运动时间为t秒(0<t<5). (1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N.
(1998•大连)如图,在直角梯形ABCD中.AD∥BC,DC⊥BC,且BC=3AD.以梯形的高AE为直径的⊙O交AB于点F,交CD于点G、H.过点F引⊙O的切线交BC于点N. BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.
BC上的动点,点G在AB上,且四边形AEFG是矩形.设FG=x,矩形AEFG的面积为y.