题目内容
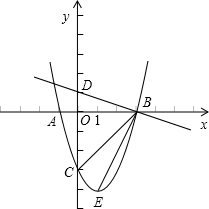 如图,抛物线y=ax2+bx-3与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.
如图,抛物线y=ax2+bx-3与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA.(I)求抛物线的解析式;
(II)探究坐标轴上是否存在点P,使得以点P,A,C为顶点的三角形为直角三角形?若存在,求出P点坐标;若不存在,请说明理由;
(III)直线y=-
| 1 | 3 |
分析:(1)易得点C坐标,根据OB=OC=3OA可得点A,B坐标.代入二次函数解析式即可.
(2)点P,A,C为顶点的三角形为直角三角形,那么应分点P,A,C三个顶点为直角顶点三种情况进行探讨.
(3)可求得E,D坐标,得到△BCE的形状,进而可把∠CBE转移为∠DBO,求解.
(2)点P,A,C为顶点的三角形为直角三角形,那么应分点P,A,C三个顶点为直角顶点三种情况进行探讨.
(3)可求得E,D坐标,得到△BCE的形状,进而可把∠CBE转移为∠DBO,求解.
解答: 解:(I)抛物线y=ax2+bx-3与y轴交于点C(0,-3),
解:(I)抛物线y=ax2+bx-3与y轴交于点C(0,-3),
∵OB=OC=3OA,
∴A(-1,0),B(3,0),代入y=ax2+bx-3,
得
,
∴y=x2-2x-3.
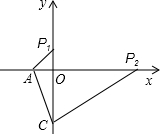
(II)①当∠P1AC=90°时,可证△P1AO∽△ACO,
∴Rt△P1AO中,tan∠P1AO=tan∠ACO=
,
∴P1(0,
).
②同理:如图当∠P2CA=90°时,P2(9,0)
③当∠CP3A=90°时,P3(0,0),
综上,坐标轴上存在三个点P,
使得以点P,A,C为顶点的三角形为直角三角形,
分别是P1(0,
),P2(9,0),P3(0,0).
(III)由y=-
x+1,得D(0,1)
由y=x2-2x-3得到顶点E(1,-4),
∴BC=3
,CE=
,BE=2
,
∵BC2+CE2=BE2,
∴△BCE为直角三角形.
∴tanβ=
=
.
又∵Rt△DOB中tan∠DBO=
=
.
∴∠DBO=∠β,
∠α-∠β=∠α-∠DBO=∠OBC=45度.
 解:(I)抛物线y=ax2+bx-3与y轴交于点C(0,-3),
解:(I)抛物线y=ax2+bx-3与y轴交于点C(0,-3),∵OB=OC=3OA,
∴A(-1,0),B(3,0),代入y=ax2+bx-3,
得
|
∴y=x2-2x-3.
(II)①当∠P1AC=90°时,可证△P1AO∽△ACO,
∴Rt△P1AO中,tan∠P1AO=tan∠ACO=
| 1 |
| 3 |
∴P1(0,
| 1 |
| 3 |
②同理:如图当∠P2CA=90°时,P2(9,0)
③当∠CP3A=90°时,P3(0,0),
综上,坐标轴上存在三个点P,
使得以点P,A,C为顶点的三角形为直角三角形,
分别是P1(0,
| 1 |
| 3 |

(III)由y=-
| 1 |
| 3 |
由y=x2-2x-3得到顶点E(1,-4),
∴BC=3
| 2 |
| 2 |
| 5 |
∵BC2+CE2=BE2,
∴△BCE为直角三角形.
∴tanβ=
| CE |
| CB |
| 1 |
| 3 |
又∵Rt△DOB中tan∠DBO=
| OD |
| OB |
| 1 |
| 3 |
∴∠DBO=∠β,
∠α-∠β=∠α-∠DBO=∠OBC=45度.
点评:通常采用待定系数法求二次函数解析式;
三角形为直角三角形,那么三个顶点都有可能为直角顶点.
三角形为直角三角形,那么三个顶点都有可能为直角顶点.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).