题目内容
已知菱形ABCD的边长为2，∠BAD=120°，则菱形的对角线长是________．
2和2
分析：已知边长及∠BAD=120°，不难求出∠ABC的度数为60°，从而进一步求得△ABC为正三角形，从而求得AC及BD的长．
解答：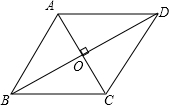
解：∵四边形ABCD是菱形，
∴AC⊥BD，∠BAO=
∠BAD=×120°=60°．
在Rt△AOB中，
∵∠ABO=90°-∠BAO=30°，
∴AO=AB=1，BO=
=，
∵AO=AC，BO=BD，
∴AC=2AO=2，BD=2BO=2．
故答案为：2和2．
点评：本题主要利用菱形的对角线互相垂直平分及勾股定理来解决．
分析：已知边长及∠BAD=120°，不难求出∠ABC的度数为60°，从而进一步求得△ABC为正三角形，从而求得AC及BD的长．
解答：
解：∵四边形ABCD是菱形，∴AC⊥BD，∠BAO=
∠BAD=×120°=60°．在Rt△AOB中，
∵∠ABO=90°-∠BAO=30°，
∴AO=
AB=1，BO==，∵AO=
AC，BO=BD，∴AC=2AO=2，BD=2BO=2
．故答案为：2和2
．点评：本题主要利用菱形的对角线互相垂直平分及勾股定理来解决．
练习册系列答案
名校课堂系列答案
相关题目
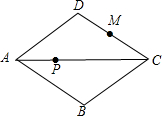如图，已知菱形ABCD的边长为6，有一内角为60°，M为CD边上的中点，P为对角线AC上的动点，则PD+PM的最小值为
面积．
如图，已知菱形ABCD的边AB=2cm，它的周长为