题目内容
如图，点A的坐标为（-1，0），点B在直线y=2x-4上运动，当线段AB最短时，点B的坐标是 ．
【答案】分析：作AB′⊥BB′，B′即为当线段AB最短时B点坐标，求出AB′的解析式，与BB′组成方程组，求出其交点坐标即可．
解答：
解：设AB′解析式为y=kx+b，
∵AB′⊥BB′，BB′解析式为y=2x-4，
∴2k=-1，
k=-
，于是函数解析式为y=-
x+b，
将A（-1，0）代入y=-
x+b得，
+b=0，b=-
，
则函数解析式为y=-
x-
，
将两函数解析式组成方程组得，
，
解得
，故B点坐标为（
，-
）．
故答案为（
，-
）．
点评：本题考查了一次函数的性质和垂线段最短，找到B′点是解题的关键，同时要熟悉待定系数法求函数解析式．
解答：
解：设AB′解析式为y=kx+b，∵AB′⊥BB′，BB′解析式为y=2x-4，
∴2k=-1，
k=-
，于是函数解析式为y=-x+b，将A（-1，0）代入y=-
x+b得，+b=0，b=-，则函数解析式为y=-
x-，将两函数解析式组成方程组得，
，解得
，故B点坐标为（，-）．故答案为（
，-）．点评：本题考查了一次函数的性质和垂线段最短，找到B′点是解题的关键，同时要熟悉待定系数法求函数解析式．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
（2012•桂平市三模）如图，点P的坐标为（2，
已知：在直角坐标系中，点C的坐标为（0，-2），点A与点B在x轴上，且点A与点B的横坐标是方程x2-3x-4=0的两个根，点A在点B的左侧．
如图，点A的坐标为（-1，0），点B在直线y=x上运动，当线段AB最短时，点B的坐标为
如图，点A的坐标为（ ）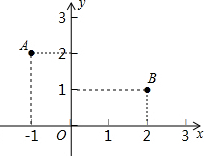
如图，点A的坐标为（-1，2），点B的坐标为（2，1），有一点C在x轴上移动，则点C到A、B两点的距离之和的最小值为（ ）