题目内容
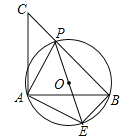
【题目】如图,已知直线l的函数表达式为y=![]() x+3,它与x轴、y轴的交点分别为A、B两点.
x+3,它与x轴、y轴的交点分别为A、B两点.
(1)若⊙O的半径为2,说明直线AB与⊙O的位置关系;
(2)若△ABO的内切圆圆心是点M,外接圆圆心是点N,则MN的长度是 ;(直接填空)
(3)设F是x轴上一动点,⊙P的半径为2,⊙P经过点B且与x轴相切于点F,求圆心P的坐标.
【答案】(1)直线AB与⊙O的位置关系是相离;(2)![]() ;(3)(
;(3)(![]() ,2).
,2).
【解析】
(1)由直线解析式求出A,B的坐标,得出OB,OA的长度,由勾股定理得出AB的长,过点O作OC⊥AB于C,由三角函数定义求出OC![]() 2,即可得出结论;
2,即可得出结论;
(2)设⊙M分别与OA、OB、AB相切于C、D、E,连接MC、MD、ME、BM,则四边形OCMD是正方形,DE⊥AB,BE=BD,得出MC=MD=ME=OD![]() (OA+OB﹣AB)=1,求出BE=BD=OB﹣OD=2,由直角三角形的性质得出△ABO外接圆圆心N在AB上,得出AN=BN
(OA+OB﹣AB)=1,求出BE=BD=OB﹣OD=2,由直角三角形的性质得出△ABO外接圆圆心N在AB上,得出AN=BN![]() AB
AB![]() ,NE=BN﹣BE
,NE=BN﹣BE![]() .在Rt△MEN中,由勾股定理即可得出答案;
.在Rt△MEN中,由勾股定理即可得出答案;
(3)连接PB、PF,作PC⊥OB于C,则四边形OCPF是矩形,得出OC=PF=BP=2,设P(x,2),由BP=2,根据两点间的距离公式列方程,解方程即可得出答案.
(1)∵直线l的函数表达式为y![]() x+3,它与x轴、y轴的交点分别为A、B两点,∴当x=0时,y=3;当y=0时,x=4;
x+3,它与x轴、y轴的交点分别为A、B两点,∴当x=0时,y=3;当y=0时,x=4;
∴A(﹣4,0),B(0,3),
∴OB=3,OA=4,
AB![]() 5,
5,
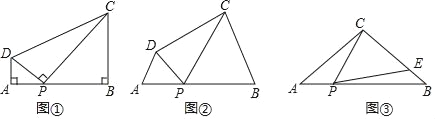
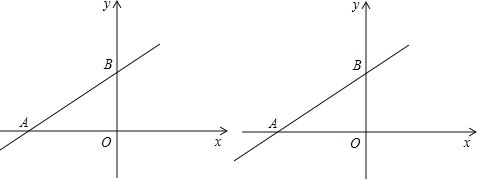
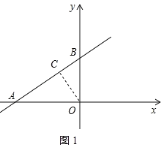
过点O作OC⊥AB于C,如图1所示:
∵sin∠BAO![]() ,∴
,∴![]() ,∴OC
,∴OC![]() 2,∴直线AB与⊙O的位置关系是相离;
2,∴直线AB与⊙O的位置关系是相离;
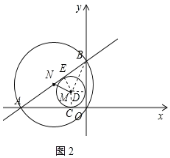
(2)设⊙M分别与OA、OB、AB相切于C、D、E,
连接MC、MD、ME、BM,如图2所示:
则四边形OCMD是正方形,DE⊥AB,BE=BD,∴MC=MD=ME=OD![]() (OA+OB﹣AB)
(OA+OB﹣AB)![]() (4+3﹣5)=1,∴BE=BD=OB﹣OD=3﹣1=2.
(4+3﹣5)=1,∴BE=BD=OB﹣OD=3﹣1=2.
∵∠AOB=90°,∴△ABO外接圆圆心N在AB上,∴AN=BN![]() AB
AB![]() ,∴NE=BN﹣BE
,∴NE=BN﹣BE![]() 2
2![]() .
.
在Rt△MEN中,MN![]() .
.
故答案为:![]() ;
;
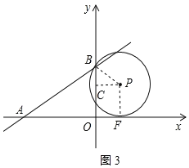
(3)连接PB、PF,作PC⊥OB于C,如图3所示:
则四边形OCPF是矩形,∴OC=PF=BP=2.
设P(x,2),由BP=2,得到:![]() ,解得:x=
,解得:x=![]() ,
,
∴圆心P的坐标为:(![]() ,2).
,2).

 备战中考寒假系列答案
备战中考寒假系列答案