题目内容

设x₁、x₂是方程3x²+4x-1=0的两根，则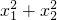 $数学公式$ =________．

$\text{[math]}$
分析：由x₁、x₂是方程3x²+4x-1=0的两根，利用根与系数的关系求出两根之和与两根之积，将所求式子利用完全平方公式变形后，将两根之和与两根之积代入即可求出值．
解答：∵x₁、x₂是方程3x²+4x-1=0的两根，
∴x₁+x₂=- $\text{[math]}$ ，x₁x₂=- $\text{[math]}$ ，
则x₁²+x₂²=（x₁+x₂）²-2x₁x₂=（- $\text{[math]}$ ）²-2×（- $\text{[math]}$ ）= $\text{[math]}$ + $\text{[math]}$ = $\text{[math]}$ ．
故答案为： $\text{[math]}$ ．
点评：此题考查了一元二次方程根与系数的关系，一元二次方程ax²+bx+c=0（a≠0），当b²-4ac≥0时，方程有解，设方程两解分别为x₁，x₂，则有x₁+x₂=- $\text{[math]}$ ，x₁x₂= $\text{[math]}$ ．