Question

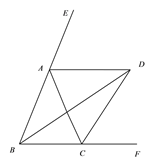
【题目】如图，四边形中， ， 平分交于， 平分交于．

求证：

Answer 1

【答案】证明见解析.

【解析】试题分析: 由四边形的内角和为360度求出∠ADC+∠ABC度数，由DF、BE分别为角平分线，利用角平分线定义及等量代换得到∠ABE+∠FDC为90度，再由直角三角形ADF两锐角互余及∠ADF=∠FDC，利用等量代换得到一对同位角相等，利用同位角相等两直线平行即可得证．

试题解析:

在四边形ABCD中

∠A+∠ABC+∠C+∠ADC=360°

又∵ ∠A=∠ C=90°

∴∠ABC+∠ ADC=180°

在Rt△AFD中，∠AFD+∠ADF=90°

又∵DF平分∠ADC

∴∠ADF=∠ADC

所以∠AFD=90°- ∠ADC=∠ABC

又∵BE平分∠ABC

∴∠ABE=∠ABC

∴∠AFD=∠ABE

∴BE//DF