题目内容
 在直角梯形ABCD中,AB∥CD,∠DAB=90°,G为AB中点,在线段DG上取点F,使FG=AG,过点F作FE⊥DG交AD于点E,连接EC交DG于点H.已知EC平分∠DEF.下列结论:①∠AFB=90°;②AF∥EC;③△EHD∽△BGF;④DH•FG=FH•DG.其中正确的是
在直角梯形ABCD中,AB∥CD,∠DAB=90°,G为AB中点,在线段DG上取点F,使FG=AG,过点F作FE⊥DG交AD于点E,连接EC交DG于点H.已知EC平分∠DEF.下列结论:①∠AFB=90°;②AF∥EC;③△EHD∽△BGF;④DH•FG=FH•DG.其中正确的是
- A.只有①②
- B.只有①②④
- C.只有③④
- D.①②③④
B
分析:由G为AB的中点,得到AG=BG,再由FG=AG,得到FG为AB的一半,根据三角形中一边上的中线等于这边的一半,可得出这边所对的角为直角,即∠AFB=90°,得到选项①正确;由EF垂直于FG,EA垂直于AG,得到一对直角相等,再由FG=AG,利用等边对等角得到一对角相等,两等式相减可得出∠EFA=∠EAF,由EC为角平分线得到一对角相等,再由∠DEF为三角形AEF的外角,利用外角的性质及等量代换可得出一对内错角相等,利用内错角相等两直线平行可得出AF与EC平行,故选项②正确;由FG=BG得到三角形BFG为等腰三角形,而三角形DEH不一定为等腰三角形,故两三角形不一定相似,选项③错误;由AF与EC平行,利用平行得比例,得到DH:HF=DE:AE,而AE=EF,等量代换得到DH:HF=DE:EF,再由一对直角相等及公共角,利用两对对应角相等的两三角形相似可得出三角形DEF与三角形DAG相似,由相似得比例得到DE:EF=DG:AG,而AG=FG,等量代换可得出DE:EF=DG:FG,等量代换变形可得出选项④正确,综上,得到所有正确的选项为①②④.
解答:∵G为AB的中点,
∴AG=BG,又FG=AG,
∴FG=AG=BG,即FG= AB,
AB,
∴∠AFB=90°,
故选项①正确;
∵FG=AG,
∴∠GFA=∠GAF,
又EF⊥FD,
∴∠EFG=∠EAG=90°,
∴∠EFG-∠GFA=∠EAG-∠GAF,即∠EFA=∠EAF,
又EC为∠DEF的平分线,
∴∠DEC=∠FEC,
∵∠DEF为△EAF的外角,
∴∠DEF=∠DEC+∠FEC=2∠FEC=∠EFA+∠EAF=2∠EFA,
∴∠FEC=∠EFA,
∴AF∥EC,
故选项②正确;
而△EHD与△BGF不一定相似,故选项③错误;
∵AF∥EC,
∴ =
= ,
,
∵∠EFD=∠GAD=90°,∠EDF=∠GDA,
∴△EFD∽△GAD,
∴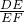 =
= ,
,
∵∠EFA=∠EAF,
∴AE=EF,又AG=FG,
∴ =
= ,
,
∴ =
= ,即DH•FG=FH•DG,
,即DH•FG=FH•DG,
故选项④正确,
综上,正确的选项有①②④.
故选B
点评:此题考查了相似三角形的判定与性质,平行线的判定与性质,等腰三角形的判定与性质,三角形的外角性质,三角形的外角性质,以及直角三角形斜边上中线性质的逆定理,熟练掌握性质及判定是解本题的关键.
分析:由G为AB的中点,得到AG=BG,再由FG=AG,得到FG为AB的一半,根据三角形中一边上的中线等于这边的一半,可得出这边所对的角为直角,即∠AFB=90°,得到选项①正确;由EF垂直于FG,EA垂直于AG,得到一对直角相等,再由FG=AG,利用等边对等角得到一对角相等,两等式相减可得出∠EFA=∠EAF,由EC为角平分线得到一对角相等,再由∠DEF为三角形AEF的外角,利用外角的性质及等量代换可得出一对内错角相等,利用内错角相等两直线平行可得出AF与EC平行,故选项②正确;由FG=BG得到三角形BFG为等腰三角形,而三角形DEH不一定为等腰三角形,故两三角形不一定相似,选项③错误;由AF与EC平行,利用平行得比例,得到DH:HF=DE:AE,而AE=EF,等量代换得到DH:HF=DE:EF,再由一对直角相等及公共角,利用两对对应角相等的两三角形相似可得出三角形DEF与三角形DAG相似,由相似得比例得到DE:EF=DG:AG,而AG=FG,等量代换可得出DE:EF=DG:FG,等量代换变形可得出选项④正确,综上,得到所有正确的选项为①②④.
解答:∵G为AB的中点,
∴AG=BG,又FG=AG,
∴FG=AG=BG,即FG=
 AB,
AB,∴∠AFB=90°,
故选项①正确;
∵FG=AG,
∴∠GFA=∠GAF,
又EF⊥FD,
∴∠EFG=∠EAG=90°,
∴∠EFG-∠GFA=∠EAG-∠GAF,即∠EFA=∠EAF,
又EC为∠DEF的平分线,
∴∠DEC=∠FEC,
∵∠DEF为△EAF的外角,
∴∠DEF=∠DEC+∠FEC=2∠FEC=∠EFA+∠EAF=2∠EFA,
∴∠FEC=∠EFA,
∴AF∥EC,
故选项②正确;
而△EHD与△BGF不一定相似,故选项③错误;
∵AF∥EC,
∴
 =
= ,
,∵∠EFD=∠GAD=90°,∠EDF=∠GDA,
∴△EFD∽△GAD,
∴
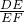 =
= ,
,∵∠EFA=∠EAF,
∴AE=EF,又AG=FG,
∴
 =
= ,
,∴
 =
= ,即DH•FG=FH•DG,
,即DH•FG=FH•DG,故选项④正确,
综上,正确的选项有①②④.
故选B
点评:此题考查了相似三角形的判定与性质,平行线的判定与性质,等腰三角形的判定与性质,三角形的外角性质,三角形的外角性质,以及直角三角形斜边上中线性质的逆定理,熟练掌握性质及判定是解本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
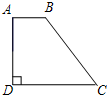 如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )
如图,在直角梯形ABCD中,AB∥DC,∠D=90°,若AD=8,BC=10,则cosC的值为( )A、
| ||
B、
| ||
C、
| ||
D、
|
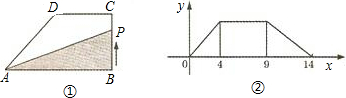
 如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD.
如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,且AB=BC=4AD,E是AB上的一点,DE⊥EC.求证:CE平分∠BCD. 如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为
如图,在直角梯形ABCD中,∠A=∠B=90°,∠C=45°,AB=4,AD=5,把梯形沿过点D的直线折叠,使点A刚好落在BC边上,则此时折痕的长为 如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )
如图,在直角梯形ABCD中,若AD=5,点A的坐标为(-2,7),则点D的坐标为( )