题目内容
观察下列各式,通过分母有理化,把不是最简二次根式的化成最简二次根式.
=
=
=
-1
=
=
=
-
同理可得:
=
-
从计算结果中找出规律,并利用这一规律计算:
+
+
+…+
(
+1)
| 1 | ||
|
1×(
| ||||
(
|
| ||
| 2-1 |
| 2 |
| 1 | ||||
|
1×(
| ||||||||
(
|
| ||||
| 3-2 |
| 3 |
| 2 |
同理可得:
| 1 | ||||
|
| 4 |
| 3 |
从计算结果中找出规律,并利用这一规律计算:
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2013 |
分析:根据题意可以得到:
+
+
+…+
(
+1)=(
-1+
-
+
-
+…+
-
)(
+1)=(
-1)(
+1),所以根据平方差公式求出即可.
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2013 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2013 |
| 2012 |
| 2013 |
| 2013 |
| 2013 |
解答:解:依题意,得
+
+
+…+
(
+1)
=(
-1+
-
+
-
+…+
-
)(
+1)
=(
-1)(
+1)
=(
)2-1,
=2012.
| 1 | ||
|
| 1 | ||||
|
| 1 | ||||
|
| 1 | ||||
|
| 2013 |
=(
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 2013 |
| 2012 |
| 2013 |
=(
| 2013 |
| 2013 |
=(
| 2013 |
=2012.
点评:本题考查了分母有理化的应用,解此题的关键是根据题目的结果找出规律,题目比较好,有一定的难度.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =
=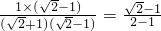 =
= -1,
-1, =
=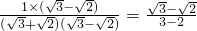 =
= -
-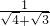 =
= -
-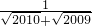 )(
)(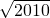 +1)的值.
+1)的值.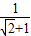 =
=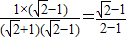 =
=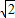 -1,
-1,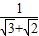 =
=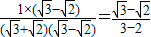 =
=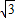 -
-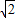 ,
, =
=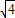 -
-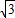 ,…
,…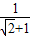 +
+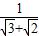 +
+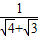 +…
+…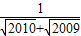 )(
)(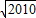 +1)的值.
+1)的值.