题目内容
分解因式:x(x-2)(x+3)(x+1)+8=________.
x+2)(x-1)(x-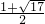 )(x-
)(x-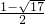 )
)
分析:分别把(x-2)和(x+3)、x和(x+1)相乘,然后变为(x2+x-6)(x2+x),接着把x2+x作为一个整体因式分解,然后即可求解.
解答:x(x-2)(x+3)(x+1)+8
=(x-2)(x+3)x(x+1)+8
=(x2+x-6)(x2+x)+8
=(x2+x)2-6(x2+x)+8
=(x2+x-2)(x2+x-4)
=(x+2)(x-1)(x-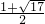 )(x-
)(x-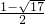 ).
).
故答案为:(x+2)(x-1)(x-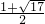 )(x-
)(x-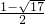 ).
).
点评:此题主要考查了利用分组分解法分解因式,解题的时候重新分组做乘法,同时也注意利用整体思想解决问题.
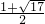 )(x-
)(x-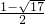 )
)分析:分别把(x-2)和(x+3)、x和(x+1)相乘,然后变为(x2+x-6)(x2+x),接着把x2+x作为一个整体因式分解,然后即可求解.
解答:x(x-2)(x+3)(x+1)+8
=(x-2)(x+3)x(x+1)+8
=(x2+x-6)(x2+x)+8
=(x2+x)2-6(x2+x)+8
=(x2+x-2)(x2+x-4)
=(x+2)(x-1)(x-
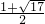 )(x-
)(x-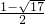 ).
).故答案为:(x+2)(x-1)(x-
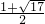 )(x-
)(x-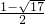 ).
).点评:此题主要考查了利用分组分解法分解因式,解题的时候重新分组做乘法,同时也注意利用整体思想解决问题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目