题目内容
等腰梯形的两底和为20，差为8，且一个底角为60°，则梯形的面积为________．
40
分析：由等腰梯形的两底和为20，差为8，可求得：上底=6，下底=14，而它有一个底角为60°，可知高=4，则梯形的面积为20×4÷2=40
解答：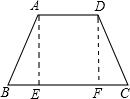
解：如图，作出梯形的高AE与DF，
∵AD+BC=20，BC-AD=8，
∴AD=6，BC=14，
∴BE=
（BC-AD）=4
又∵∠B=60°
∴AE=tan60°•BE=4，
∴梯形的面积为：（AD+BC）AE÷2=20×4÷2=40
点评：此题考查等腰梯形的性质、面积计算和等边三角形的性质等知识点．
分析：由等腰梯形的两底和为20，差为8，可求得：上底=6，下底=14，而它有一个底角为60°，可知高=4
，则梯形的面积为20×4÷2=40解答：
解：如图，作出梯形的高AE与DF，∵AD+BC=20，BC-AD=8，
∴AD=6，BC=14，
∴BE=
（BC-AD）=4又∵∠B=60°
∴AE=tan60°•BE=4
，∴梯形的面积为：（AD+BC）AE÷2=20×4
÷2=40点评：此题考查等腰梯形的性质、面积计算和等边三角形的性质等知识点．
练习册系列答案
相关题目