题目内容
 如图,以正方形ABCD的一边AD为直径向内作半圆AED,已知Rt△EFD的面积为1,那么曲边四边形ABCDE(阴影部分)的面积是
如图,以正方形ABCD的一边AD为直径向内作半圆AED,已知Rt△EFD的面积为1,那么曲边四边形ABCDE(阴影部分)的面积是分析:由半圆AED与Rt△EFD的面积为1,根据直角三角形的面积求解方法,即可求得半圆AED的半径,则可得正方形的边长AD的长,然后由S曲边四边形ABCDE=S正方形ABCD-S半圆AED即可求得答案.
解答:解:设半圆AED的半径为r,
∵Rt△EFD的面积为1,
即SRt△EFD=
DE•EF=
r2=1,
∴r=
,
∴AD=2r=2
,
∴S曲边四边形ABCDE=S正方形ABCD-S半圆AED=(2
)2-
π×(
)2=8-π≈4.86.
故答案为:4.86.
∵Rt△EFD的面积为1,
即SRt△EFD=
| 1 |
| 2 |
| 1 |
| 2 |
∴r=
| 2 |
∴AD=2r=2
| 2 |
∴S曲边四边形ABCDE=S正方形ABCD-S半圆AED=(2
| 2 |
| 1 |
| 2 |
| 2 |
故答案为:4.86.
点评:此题考查了半圆,正方形与直角三角形的面积的求解方法.此题难度适中,解题的关键是注意数形结合思想与方程思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=
13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=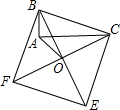 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO= 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( ) 如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )
如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )