题目内容
已知反比例函数 的图象经过点P(2,2)、Q(4,m).直线y=ax+b与直线y=-x平行,并且经过点Q.
的图象经过点P(2,2)、Q(4,m).直线y=ax+b与直线y=-x平行,并且经过点Q.
(1)求直线y=ax+b的解析式;
(2)当x为何值时,函数 取得最大值或最小值?并求出这个最大值或最小值.
取得最大值或最小值?并求出这个最大值或最小值.
解:(1)∵函数 的图象经过点P(2,2),
的图象经过点P(2,2),
∴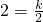 .
.
∴k=4.
∴反比例函数为 .
.
又∵Q(4,m)在反比例函数 的图象上,
的图象上,
∴m=1.
∴Q(4,1).
∵直线y=ax+b与y=-x平行,
∴a=-1.
∴直线的解析式为y=-x+b.
又∵直线y=-x+b过Q(4,1),
∴1=-4+b.
b=5.
∴直线的解析式为y=-x+5;
(2)由a=-1,b=5,k=4,
得函数 为
为 .
.
∴ =
= =
= ,
,
= ,
,
∴当 时,所求函数的最大值为1.
时,所求函数的最大值为1.
分析:(1)由反比例函数 的图象经过点P(2,2)可以求出反比例函数解析式,从而得出Q(4,m)的坐标,直线y=ax+b与直线y=-x平行,可得出a=-1,并且经过点Q,从而求出解析式;
的图象经过点P(2,2)可以求出反比例函数解析式,从而得出Q(4,m)的坐标,直线y=ax+b与直线y=-x平行,可得出a=-1,并且经过点Q,从而求出解析式;
(2)由(1)式中a,b,k的值得出二次函数的解析式,可以借助配方法求出二次函数的最值.
点评:此题主要考查了一次函数与反比例函数和二次函数综合题目,综合性较强,两问中层层递进,在计算过程中一定注意认真避免出错.
 的图象经过点P(2,2),
的图象经过点P(2,2),∴
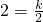 .
.∴k=4.
∴反比例函数为
 .
.又∵Q(4,m)在反比例函数
 的图象上,
的图象上,∴m=1.
∴Q(4,1).
∵直线y=ax+b与y=-x平行,
∴a=-1.
∴直线的解析式为y=-x+b.
又∵直线y=-x+b过Q(4,1),
∴1=-4+b.
b=5.
∴直线的解析式为y=-x+5;
(2)由a=-1,b=5,k=4,
得函数
 为
为 .
.∴
 =
= =
= ,
,=
 ,
,∴当
 时,所求函数的最大值为1.
时,所求函数的最大值为1.分析:(1)由反比例函数
 的图象经过点P(2,2)可以求出反比例函数解析式,从而得出Q(4,m)的坐标,直线y=ax+b与直线y=-x平行,可得出a=-1,并且经过点Q,从而求出解析式;
的图象经过点P(2,2)可以求出反比例函数解析式,从而得出Q(4,m)的坐标,直线y=ax+b与直线y=-x平行,可得出a=-1,并且经过点Q,从而求出解析式;(2)由(1)式中a,b,k的值得出二次函数的解析式,可以借助配方法求出二次函数的最值.
点评:此题主要考查了一次函数与反比例函数和二次函数综合题目,综合性较强,两问中层层递进,在计算过程中一定注意认真避免出错.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知反比例函数的图象经过点(a,b),则它的图象一定也经过( )
| A、(-a,-b) | B、(a,-b) | C、(-a,b) | D、(0,0) |