题目内容
直角三角形纸片的两直角边长分别为6，8，现将△ABC如图那样折叠，使点A与点B重合，折痕为DE，则tan∠CBE的值是 ．
【答案】分析：折叠后形成的图形相互全等，设BE=x，则CE=8-x，在RT△BCE中利用勾股定理求出BE，利用三角函数的定义可求出．
解答：解：根据题意，BE=AE．设BE=x，则CE=8-x．
在Rt△BCE中，x2=（8-x）2+62，
解得x=
，故CE=8-
=
，
∴tan∠CBE=
=
．
故答案为：
．
点评：本题考查锐角三角函数的概念：在直角三角形中，正弦等于对边比斜边；余弦等于邻边比斜边；正切等于对边比邻边．
解答：解：根据题意，BE=AE．设BE=x，则CE=8-x．
在Rt△BCE中，x2=（8-x）2+62，
解得x=
，故CE=8-=，∴tan∠CBE=
=．故答案为：
．点评：本题考查锐角三角函数的概念：在直角三角形中，正弦等于对边比斜边；余弦等于邻边比斜边；正切等于对边比邻边．
练习册系列答案
相关题目
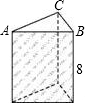如图，是一个直三棱柱的模型，其底面是两直角边长分别为3cm、4cm的直角三角形，侧棱长都是8cm．
如图，是一个直三棱柱的模型，其底面是两直角边长分别为3cm、4cm的直角三角形，侧棱长都是8cm．