题目内容

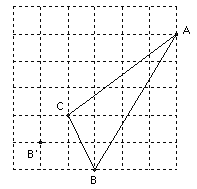
如图所示，⊙O′过点O，A，B，O（0，0），A（0，2），B（2，0），圆上一动点P．
（1）求∠OPB；（2）当P到OB距离最远时，求P点坐标及△POB的面积．

解：（1）∠OPB=∠OAB，∵AB是⊙O直径，
∴∠AOB=90°，AO=OB=2，∠OAB=45°，∠OAB=∠OPB=45°．

（2）如图，当P运动到距离OB最高时，
作OB中垂线交⊙O于P，N，交OB于C，PC＞NC，PC最长．
∵AB= $\text{[math]}$ =2 $\text{[math]}$ ．OC= $\text{[math]}$ OB= $\text{[math]}$ ×2=1．∴O′C= $\text{[math]}$ =1，
∴P（1，1+ $\text{[math]}$ ）．S_△OPB= $\text{[math]}$ •PC•OB= $\text{[math]}$ ×2×（1+ $\text{[math]}$ ）=1+ $\text{[math]}$ ．
分析：（1）根据同弧所对的圆周角相等，即可求得∠OAB的度数．根据所给的坐标发现等腰直角三角形；
（2）根据圆的轴对称性，当P到弦的垂直平分线和优弧的交点时和OB的距离最远．根据垂径定理的推论知弦的垂直平分线必过圆心，只需进一步求得O′C的长．
点评：此题中主要是能够根据点的坐标发现特殊三角形求解．

练习册系列答案

（本题10分）在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示.

（1）过点B′画出平移后的△A′B′C′，使A′和A、B′和B、C′和C分别对应；

（2）若连接AA′、BB′、CC′，则这三条线段之间的关系是______ ，仔细观察，图中互相平行的线段共有对；

（3）求△A′B′C′的面积．

（本题10分）在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示.

（1）过点B′画出平移后的△A′B′C′，使A′和A、B′和B、C′和C分别对应；
（2）若连接AA′、BB′、CC′，则这三条线段之间的关系是______ ，仔细观察，图中互相平行的线段共有对；
（3）求△A′B′C′的面积．

（本题10分）在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示.

（1）过点B′画出平移后的△A′B′C′，使A′和A、B′和B、C′和C分别对应；
（2）若连接AA′、BB′、CC′，则这三条线段之间的关系是______ ，仔细观察，图中互相平行的线段共有对；
（3）求△A′B′C′的面积．

将一幅三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F．

（1）求证：CF∥AB．

（2）求∠DFC的度数．

如图所示，⊙O′过点O，A，B，O（0，0），A（0，2），B（2，0），圆上一动点P．（1）求∠OPB；（2）当P到OB距离最远时，求P点坐标及△POB的面积．

试题分类

如图所示，⊙O′过点O，A，B，O（0，0），A（0，2），B（2，0），圆上一动点P．
（1）求∠OPB；（2）当P到OB距离最远时，求P点坐标及△POB的面积．