Question

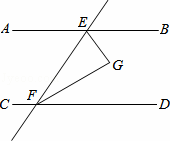
如图所示，直线AB∥CD，直线AB、CD被直线EF所截，EG平分∠BEF，FG平分∠DFE，

（1）若∠AEF=50°，求∠EFG的度数．

（2）判断EG与FG的位置关系，并说明理由．

Answer 1

考点：

平行线的性质．

专题：

探究型．

分析：

（1）先根据平行线的性质得出∠EFD=∠AEF=50°，再由FG平分∠DFE即可得出结论；

（2）先由AB∥CD得出∠BEF+∠EFD=180°，再根据EG平分∠BEF，FG平分∠DFE可得出∠GEF+∠GFE的度数，根据三角形内角和定理即可得出结论．

解答：

解：（1）∵AB∥CD

∴∠EFD=∠AEF=50°，

∵FG平分∠DFE，

∵∠EFG=∠DFE=×50°=25°；（2）EG⊥FG．

理由：∵AB∥CD，

∴∠BEF+∠EFD=180°，

∵EG平分∠BEF，FG平分∠DFE，

∴∠GEF=∠BEF，∠GFE=∠DFE，

∴∠GEF+∠GFE=∠BEF+∠DFE，

=（∠BEF+∠DFE）

=×180°

=90°，

∴∠G=180°﹣（∠BEF+∠DFE）=90°

∴EG⊥FG．

点评：

本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．