题目内容
【题目】如图,在长方形ABCD中,AB=4cm,BC=8cm.E、F分别是AB、BC的中点.则E到DF的距离是cm.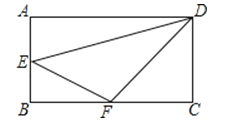
【答案】![]()
【解析】解:∵四边形ABCD是矩形,
∴CD=AB=4cm,AD=BC=8cm,∠A=∠B=∠C=∠D=90°,
∵E、F分别是AB、BC的中点,
∴AE=BE=![]() AB=2cm,BF=CF=
AB=2cm,BF=CF=![]() BC=4cm,
BC=4cm,
∴DF=![]() =4
=4![]() (cm),
(cm),
∴△DEF的面积=矩形ABCD的面积﹣△BEF的面积﹣△CDF的面积﹣△ADE的面积
=8×4﹣![]() ×4×2﹣
×4×2﹣![]() ×4×4﹣
×4×4﹣![]() ×8×2
×8×2
=12(cm2),
作EG⊥DF于G,如图所示:
则△DEF的面积=![]() DFEG=12,
DFEG=12,
∴EG=![]() =
=![]() (cm),
(cm),
即E到DF的距离是![]() cm,
cm,
所以答案是:![]() .
. 
【考点精析】认真审题,首先需要了解矩形的性质(矩形的四个角都是直角,矩形的对角线相等).

练习册系列答案
相关题目