题目内容
已知:如图,⊙![]() 与
与![]() 轴交于C、D两点,圆心
轴交于C、D两点,圆心![]() 的坐标为(1,0),⊙
的坐标为(1,0),⊙![]() 的半径为
的半径为![]() ,过点C作⊙
,过点C作⊙![]() 的切线交
的切线交![]() 轴于点B(-4,0)
轴于点B(-4,0)
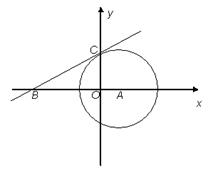
1.求切线BC的解析式;
2.若点P是第一象限内⊙![]() 上一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点
上一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点![]() 的坐标;
的坐标;
3.向左移动⊙![]() (圆心
(圆心![]() 始终保持在
始终保持在![]() 轴上),与直线BC交于E、F,在移动过程中是否存在点
轴上),与直线BC交于E、F,在移动过程中是否存在点![]() ,使得△AEF是直角三角形?若存在,求出点
,使得△AEF是直角三角形?若存在,求出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
1.(1)连接![]() ,∵
,∵![]() 是⊙A的切线,∴
是⊙A的切线,∴![]() .
.
∴![]() .
.
∵![]() ,∴
,∴![]() ,∴
,∴![]() .
.
∴△![]() ∽△
∽△![]() ,∴
,∴![]() .
.
即![]() ,∴
,∴![]() .∴
.∴![]() 点坐标是(0,2).
点坐标是(0,2).
设直线![]() 的解析式为
的解析式为![]() ,∵该直线经过点B(-4,0)与点
,∵该直线经过点B(-4,0)与点![]() (0,2),
(0,2),
∴![]() 解得
解得![]()
∴该直线解析式为![]()
2.连接![]() ,过点
,过点![]() 作
作![]() .
.

由切线长定理知
 .
.
在![]() 中,∵
中,∵![]() ,
,
∴![]() .
.
在![]() 中,由勾股定理得
中,由勾股定理得
 .
.
∴ ![]() .
.
又∵![]() .
.
∴![]() ∽
∽![]() ,∴
,∴![]() ,
,
∴ .
.
则![]() 是点
是点![]() 的纵坐标,
的纵坐标,
∴![]() ,解得
,解得![]() .
.
∴点![]() 的坐标
的坐标![]() .
.
3.)如图示,当![]() 在点
在点![]() 的右侧时
的右侧时

∵![]() 、
、![]() 在⊙
在⊙![]() 上,∴
上,∴![]() .
.
若△![]() 是直角三角形,则
是直角三角形,则![]() ,且为等腰直角三角形.
,且为等腰直角三角形.
过点![]() 作
作![]() ,在
,在![]() 中由三角函数可知
中由三角函数可知
 .
.
又∵![]() ∽
∽![]() ,
,
∴![]() ,
,
∴ .
.
∴![]() ,
,
∴点![]() 坐标是
坐标是![]() .
.
当![]() 在点
在点![]() 的左侧时:同理可求点
的左侧时:同理可求点![]() 坐标是
坐标是![]()
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
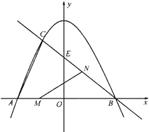
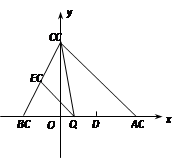
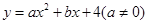 与
与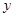 轴交于点
轴交于点 ,与
,与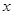 轴交于点
轴交于点 ,点
,点 的坐标为
的坐标为 ,对称轴是
,对称轴是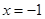 .
. 是线段
是线段 上的动点,过点
上的动点,过点 ∥
∥ ,分别交
,分别交 于点P、
于点P、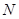 ,连接
,连接 .当
.当 的面积最大时,求点
的面积最大时,求点 的值.
的值.
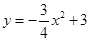 与
与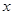 轴交于点
轴交于点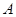 ,点
,点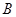 ,与直线
,与直线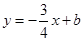 相交于点
相交于点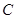 ,直线
,直线 轴交于点
轴交于点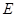 .
.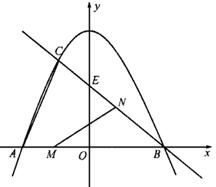
 的面积.
的面积.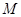 在线段
在线段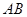 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从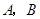 重合),同时,点
重合),同时,点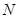 在射线
在射线 上以每秒2个单位长度的速度从
上以每秒2个单位长度的速度从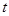 秒,请写出
秒,请写出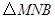 的面积
的面积 与
与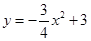 与
与 轴交于点
轴交于点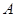 、点
、点 ,与直线
,与直线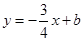 相交于点
相交于点 ,直线
,直线 轴交于点
轴交于点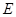 。
。
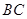 的解析式;
的解析式;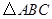 的面积;
的面积; 在线段
在线段 上以每秒1个单位长度的速度从
上以每秒1个单位长度的速度从 重合),同时,点
重合),同时,点 在射线
在射线 秒,请写出
秒,请写出 的面积
的面积 与
与