题目内容
 如图,小李晚上由路灯A下的B处走到C时,测得影子CD的长为2米,继续往前走5米到达E处时,测得影子EF的长为3米,已知小李的身高CM为1.8米,求路灯A的高度AB.
如图,小李晚上由路灯A下的B处走到C时,测得影子CD的长为2米,继续往前走5米到达E处时,测得影子EF的长为3米,已知小李的身高CM为1.8米,求路灯A的高度AB.
解:∵ ,
,
当小李在CM处时,Rt△DCM∽Rt△DBA,即 =
=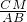 ,
,
当小李在EN处时,Rt△FEN∽Rt△FBA,即 =
= =
=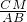 ,
,
∴ =
= ,
,
∵CM=EN=1.8米,CD=2米,CE=5米,EF=3米,
设AB=x米,BC=y米,
∴ =
= ,
,
解得y=10米,
∵ =
=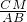
∴ ,
,
解得x=10.8米.
∴路灯AB的高度为10.8米.
分析:根据在同一时刻物高和影长成正比,即在同一时刻的两个物体、影子、经过物体顶部的光线三者构成的两个直角三角形相似解答即可.
点评:本题综合考查了中心投影的特点和规律以及相似三角形性质的运用.解题的关键是利用中心投影的特点可知在这两组相似三角形中有一组公共边,利用其作为相等关系求出所需要的线段,再求公共边的长度.
 ,
,当小李在CM处时,Rt△DCM∽Rt△DBA,即
 =
=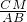 ,
,当小李在EN处时,Rt△FEN∽Rt△FBA,即
 =
= =
=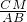 ,
,
∴
 =
= ,
,∵CM=EN=1.8米,CD=2米,CE=5米,EF=3米,
设AB=x米,BC=y米,
∴
 =
= ,
,解得y=10米,
∵
 =
=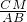
∴
 ,
,解得x=10.8米.
∴路灯AB的高度为10.8米.
分析:根据在同一时刻物高和影长成正比,即在同一时刻的两个物体、影子、经过物体顶部的光线三者构成的两个直角三角形相似解答即可.
点评:本题综合考查了中心投影的特点和规律以及相似三角形性质的运用.解题的关键是利用中心投影的特点可知在这两组相似三角形中有一组公共边,利用其作为相等关系求出所需要的线段,再求公共边的长度.

练习册系列答案
相关题目
 如图,小李晚上由路灯A下的B处走到C时,测得影子CD的长为2米,继续往前走5米到达E处时,测得影子EF的长为3米,已知小李的身高CM为1.8米,求路灯A的高度AB.
如图,小李晚上由路灯A下的B处走到C时,测得影子CD的长为2米,继续往前走5米到达E处时,测得影子EF的长为3米,已知小李的身高CM为1.8米,求路灯A的高度AB.

