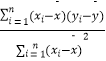题目内容
【题目】在如图所示的几何体中，平面ADNM⊥平面ABCD，四边形ABCD是菱形，ADNM是矩形， 
，AB=2，AM=1，E是AB的中点． 
（1）求证：平面DEM⊥平面ABM；
（2）在线段AM上是否存在点P，使二面角P﹣EC﹣D的大小为 
？若存在，求出AP的长；若不存在，请说明理由．
【答案】
（1）证明：∵ABCD是菱形，∴AD=AB，∵∠DAB=60°，∴△ABD为等边三角形，
E为AB中点，∴DE⊥AB，∴DE⊥CD，
∵ADMN是矩形，∴ND⊥AD，
又平面ADMN⊥平面ABCD，平面ADMN∩平面ABCD=AD，
∴ND⊥平面ABCD，∴ND⊥DE，
∵CD∩ND=D，∴DE⊥平面NDC，
∵DE平面MDE，∴平面MDE⊥平面NDC．
因为面ABM∥面NDC，∴平面DEM⊥平面ABM
（2）解：设存在P符合题意．
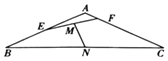
由（Ⅰ）知，DE、DC、DN两两垂直，以D为原点，建立空间直角坐标系D﹣xyz（如图），
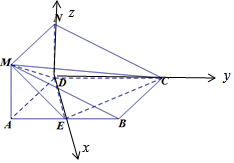
则D（0，0，0），A（ 
，﹣1，0），E（ ，0，0），C（0，2，0），P（ ，﹣1，h）（0≤h≤1）．
∴ 
=（0，﹣1，h）， 
=（﹣ ，2，0），设平面PEC的法向量为 
=（x，y，z），
则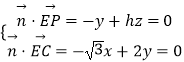 
令x=2h，则平面PEC的一个法向量为 =（2h， h， ）
取平面ECD的法向量 
=（0，0，1），
cos45°= 
，解得h= 
∈[0，1]，
即存在点P，使二面角P﹣EC﹣D的大小为 
，此时AP= ．
【解析】（1）推导出DE⊥CD，ND⊥AD，从而ND⊥DE，进而DE⊥平面NDC，由此能证明平面MAE⊥平面NDC．（2）以D为原点，建立空间直角坐标系D﹣xyz，求出平面PEC的一个法向量、平面ECD的法向量．利用向量的夹角公式，建立方程，即可得出结论．
