Question

若∠C=，∠EAC+∠FBC=
（1）如图①，AM是∠EAC的平分线，BN是∠FBC的平分线，若AM∥BN，则与有何关系？并说明理由．

（2）如图②，若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P，试探究∠APB与、的关系是                                       ．(用、表示)

（3）如图③，若≥，∠EAC与∠FBC的平分线相交于， ;依此类推，则=                 (用、表示）

Answer 1

（1）=；
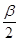（2）∠APB=﹣；
（3）∠A P₅B=﹣．

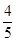
解析试题分析：（1）过点C作CD∥AM，根据平行线相关定理即可；
（2）利用三角形外角进行计算即可；
（3）类比（2）的做法进行计算．
试题解析：（1）过点C作CD∥AM，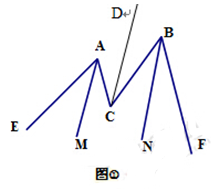

∵AM∥BN，
∴CD∥AM∥BN，
∴∠ACD=∠MAC，
∠BCD=∠CBN，
∴=∠ACD+∠BCD =∠MAC +∠CBN=(∠EAC+∠FBC)=，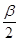
∴=；
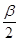（2）如图所示：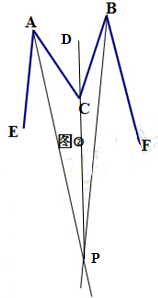

P

 

∵∠EAC的平分线所在直线与∠FBC平分线所在直线交于P，
∴∠CAP+∠CBP =(∠EAC+∠FBC)=
∵∠ACD=∠CAP+∠APC，∠BCD=∠CAB+∠BPC，
∴∠ACB=∠ACD+∠BCD = (∠APC+∠BPC）+ (∠CAP+∠CAB）= ∠APB+
∴∠APB=﹣；
（3）连接P₅C并延长至点D，
根据题意知：∠CAP₅+∠CBP₅ =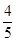(∠EAC+∠FBC)=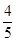
∵∠ACD=∠CA P₅+∠A P₅C，∠BCD=∠CAB+∠B P₅C，
∴∠ACB=∠ACD+∠BCD = (∠A P₅C+∠B P₅C）+ (∠CA P₅+∠CAB）= ∠A P₅B+
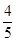
∴∠A P₅B=﹣．
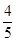
考点：角平分线．